Cho tam giác ABC, phân giác BD. Qua D kẻ đường thẳng vuông góc với BC tại E
a, Chứng minh tam giác BAD =tam giác BED
b, CM BD là đường trung trực của AE
c, Trên tia đối của tia AB lấy điểm F sao cho AF=CE. Chứng minh E,D,F thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 8 2015
a. Xét tam giác ABD vuông tại A và tam giác BED vuông tại E có:
BD : Cạnh chung
Góc ABD = góc DBE (BD phân giác)
=> Tam giác ABD = tam giác BED (cạnh huyền - góc nhọn)
b. Ta có BA = BE (Tam giác = tam giác câu a)
=> tam giác BAE cân tại B.
Lại có BD là phân giác tam giác BAE => BD vừa là phân giác vừa là đường trung trực của đoạn AE.
c. Xét tam giác EDC vuông tại E:
DE < DC (Cạnh góc vuông nhỏ hơn cạnh huyền)
Mà DE = DA (Tam giác = tam giác câu a)
=> DA < DC.
d. Xét tam giác ADF và tam giác EDC:
DA = DE (tam giác = tam giác câu a)
DAF = DEC (=90 độ)
AF = EC (gt)
=> Tam giác ADF = tam giác EDC (C.g.c)
=> ADF = EDC (góc tương ứng)
Mặt khác : EDC + EDA = 180 độ .
Từ đó suy ra : EDA + ADF = 180 độ.
Vậy E,D,F thẳng hàng.
6 tháng 5 2016
Cách 1: Giải theo phương pháp bậc tiểu học (của bạn Ác Quỷ)
Ta có
Mà dt(AMN) = 1/4 dt(ABN) = 1/4 . 1/2 dt(ABC) = 1/8 dt(ABC)
dt(DMN) = dt(ABC) - dt(AMN) - dt(BDM) - dt(CDN) = dt(ABC) - 1/8 dt(ABC) - 3/8 dt(ABC) - 1/4 dt(ABC) = 1/4 dt(ABC)
Vậy , suy ra AE/AD = 1/3
Cách 2: Giải theo phương pháp bậc THCS (của bạn Lê Quang Vinh)
DN là đường trung bình của tam giác ABC => DN // AB và DN = 1/2 AB
DN // AB => Hai tam giác EAM và EDN đồng dạng => EA/ED = AM/DN = 1/2 (vì AM = 1/4 AB, DN = 1/2 AB)
=> AE/AD = 1/3
28 tháng 4 2016
a) Vì tam giác ABC vuông tại A(gt)
=)Â=90 độ
=)tam giác BAD là tam giác vuông tại A
Vì DE vuông góc vs BC (gt)
=)Ê =90 độ
=)tam giác BED là tam giác vuông tại E
xét tam giác BAD vuông tại A và tam giác BED vuông tại E có
Góc ABD =Góc EBD(vì BD là tia phân giác)
BD là cạnh chung
=) tam giác BAD=tam giác BED(ch-cgv)
28 tháng 4 2016
Xét 2 tam giác vuông ABD và EBD có
Góc ABD=góc EBD(gt)
Cạnh huyền BD chung
=)) tam giác ABD=tam giácEBD (ch-gn)
18 tháng 8 2021
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE và DA=DE
Ta có: BA=BE
nên B nằm trên đường trung trực của AE\(\left(1\right)\)
Ta có: DA=DE
nên D nằm trên đường trung trực của AE\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra BD là đường trung trực của AE
19 tháng 8 2021
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
AF=EC
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
hay ΔDFC cân tại D
16 tháng 5 2023
Mình xin phép sửa lại đề (ý c,)
c) Trên tia đối của tia AB lấy điểm F sao cho AF = EC. Chứng minh `Δ`BFC cân
`a,`
Xét `2\Delta` vuông `ABD` và `EBD`:
`\text {BD chung}`
$\widehat {ABD} = \widehat {EBD} (\text {tia phân giác} \widehat {ABE})$
`=> \Delta ABD = \Delta EBD (ch-gn)`
`b,`
Vì `\Delta ABD = \Delta EBD (a)`
`-> \text {DA = DE (2 cạnh tương ứng) (1)}`
Xét `\Delta DEC`:
$\widehat {DEC} = 90^0$
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`-> \text {DC là cạnh lớn nhất}`
`-> \text {DC > DE (2)}`
Từ `(1)` và `(2)`
`-> \text {DC > DA}`
`c,`
Xét `2\Delta` vuông `ABC` và `AFC`:
`\text {AB = AF (gt)}`
$\widehat {BAC} = \widehat {FAC} (=90^0)$
`\text {AC chung}`
`=> \Delta ABC = \Delta AFC (c-g-c)`
`-> \text {BC = FC (2 cạnh tương ứng)}`
Xét `\Delta BFC`:
`\text {BC = FC}`
`-> \Delta BFC` cân tại C.
`d,`
Ta có: FE là đường cao của `\Delta BFC`
`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`
`-> \text {FE đồng thời cũng là đường trung trực}`
`-> \text {Ba điểm F, D, E thẳng hàng.}`
16 tháng 5 2023
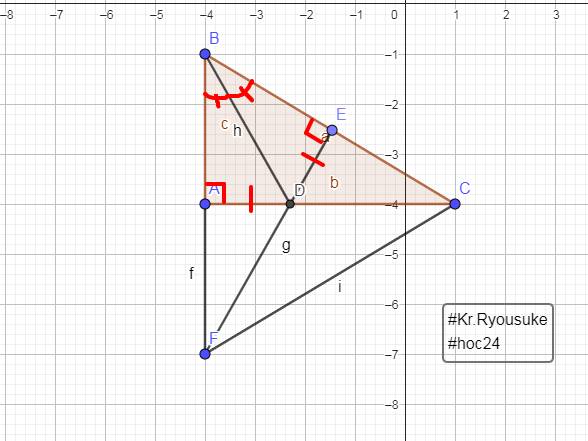
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: DA=DE
DE<DC
=>DA<DC
c: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D