| 6 | 2 | 4 | 1 | 2 | 6 | 2 |
| 2 | 4 | 7 | 2 | 5 | 5 | 2 |
Số đơn vị điều tra là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Mức lương bình quân của các cán bộ và nhân viên công ty là số trung bình của bảng lương:
- Số trung bình:
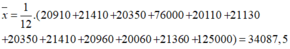
Sắp xếp các số liệu theo dãy tăng dần:
20060; 20110; 20350; 20350; 20910; 20960; 21130; 21360; 21410; 21410; 76000; 125000.
Số trung vị: Me = (20960 + 21130)/2 = 21045.
Ý nghĩa: Số trung vị đại diện cho mức lương trung bình của nhân viên (vì trong trường hợp này chênh lệch giữa các số liệu quá lớn nên không thể lấy mức lương bình quân làm giá trị đại diện).

- Mức lương bình quân của các cán bộ và nhân viên công ty là số trung bình của bảng lương:
Ý nghĩa: Số trung vị phân chia dãy số liệu sắp thứ tự thành hai phần bằng nhau.

Chọn A.
Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A
Liệt kê số điểm của 44 học sinh lớp 10A nên kích thước mẫu của số liệu là 44.

Bảng phân bố tần số
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 50 | 54 | cộng |
| Tần số | 4 | 5 | 20 | 10 | 8 | 3 | 50 |
Bảng phân bố tần suất
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 20 | 54 | Cộng |
| Tần suất (%) | 8 | 10 | 40 | 20 | 16 | 6 | 100% |

Trong bảng phân bố trên, hai giá trị 700 và 900 có cùng tần số lớn nhất là 6. Do đó ta có hai mốt là:
M0(1) = 700; M0(2) = 900.
Ý nghĩa:
+ Số công nhân có tiền lương 700.000đ/tháng và 900.000đ/tháng bằng nhau và chiếm đa số.
+ Tỉ lệ công nhân có mức lương 700 nghìn đồng / tháng và 900 nghìn đồng/ tháng cao hơn tỉ lệ công nhân có các mức lương khác.

| Bậc lương (x) | 1 | 2 | 3 | 5 | 6 | 7 | |
| Tần số (n) | 4 | 2 | 1 | 5 | 6 | 2 | N = 20 |
Tần số bé nhất là: 2
TK MK NHA MK ĐANG BỊ ÂM ĐIỂM
xloi cậu tần số bé nhất là 1 mới đúng mk ghi lộn

a) Nhà máy A:
+) Số trung bình: \(\overline x = \frac{{4 + 5 + 5 + 47 + 5 + 6 + 4 + 4}}{8} = 10\)
+) Mốt: \({M_o} = 4,{M_o} = 5\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 4; 4; 4; 5; 5; 5; 6; 47.
\({Q_2} = {M_e} = 5\)
\({Q_1}\) là trung vị của nửa số liệu: 4; 4; 4; 5. Do đó \({Q_1} = 4\)
\({Q_3}\) là trung vị của nửa số liệu: 5; 5; 6; 47. Do đó \({Q_3} = 5,5\)
+) Phương sai \({S^2} = \frac{1}{8}\left( {{4^2} + {5^2} + ... + {4^2}} \right) - {10^2} = 196\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 14\)
Nhà máy B:
+) Số trung bình: \(\overline x = \frac{{2 + 9 + 9 + 8 + 10 + 9 + 9 + 11 + 9}}{9} = 8,4\)
+) Mốt: \({M_o} = 9\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 2; 8; 9; 9; 9; 9; 9; 10; 11
\({Q_2} = {M_e} = 9\)
\({Q_1}\) là trung vị của nửa số liệu: 2; 8; 9; 9. Do đó \({Q_1} = 8,5\)
\({Q_3}\) là trung vị của nửa số liệu: 9; 9; 10; 11. Do đó \({Q_3} = 9,5\)
+) Phương sai \({S^2} = \frac{1}{9}\left( {{2^2} + {9^2} + ... + {9^2}} \right) - 8,{4^2} = 6,55\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 2,56\)
b)
Nhà máy A có: \({\Delta _Q} = 1,5\)
Vậy giá trị ngoại lệ \(x > 5,5 + 1,5.1,5 = 7,75\) hoặc \(x < 4 - 1,5.1,5 = 1,75\) là 47.
Nhà máy B có: \({\Delta _Q} = 1\)
Vậy giá trị ngoại lệ \(x > 9,5 + 1,5.1 = 11\) hoặc \(x < 8,5 - 1,5.1 = 7\) là 2.
Ta so sánh trung vị: \(9 > 5\), do dó công nhân nhà máy B có mức lương cao hơn.
Chú ý
Ta không so sánh số trung bình vì có giá trị 47 quá lớn so với các giá trị còn lại.