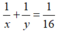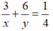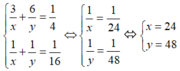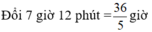HAI NGƯỜI THỢ CÙNG LÀM MỘT CÔNG VIỆC TRONG 7H12P THÌ XONG NẾU NGƯỜI THỨ NHẤT LÀM TRONG 4H VÀ NGƯỜI THỨ HAI LÀM TRONG 3H THÌ HỌ LÀM ĐƯỢC 50% CÔNG VIỆC HỎI MỖI NGƯỜI LÀM MỘT MÌNH CÔNG VIỆC ĐÓ TRONG BAO LÂU
GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH GIÚP MK NHÉ