Tính tích: A=\(\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{9}\right)...\left(1-\dfrac{1}{10000}\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TC
26 tháng 3 2022
\(=\left(\dfrac{4}{4}-\dfrac{1}{4}\right)\left(\dfrac{9}{9}-\dfrac{1}{9}\right)\left(\dfrac{16}{16}-\dfrac{1}{16}\right)...\left(\dfrac{10000}{10000}-\dfrac{1}{10000}\right)\)
\(=\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot\dfrac{15}{16}....\cdot\dfrac{9999}{10000}\)
\(=\dfrac{3.8.15.....9999}{4.9.16.....10000}=\dfrac{\left(1.3\right)\left(2.4\right)\left(3.5\right)....\left(99.101\right)}{\left(2.2\right)\left(3.3\right)\left(4.4\right).....\left(100.100\right)}\)
\(=\dfrac{\left(1.2.3...99\right)\left(3.4.5....101\right)}{\left(2.3.4...100\right)\left(2.3.4...101\right)}=\dfrac{101.1}{100.2}=\dfrac{101}{200}\)
30 tháng 10 2023
\(E=\dfrac{\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{2002}-1\right)\left(\dfrac{1}{2003}-1\right)}{\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot...\cdot\dfrac{9999}{10000}}\)
\(=\dfrac{\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2002}\right)\left(1-\dfrac{1}{2003}\right)}{\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{100^2}\right)}\)
\(=\dfrac{\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2002}\right)\left(1-\dfrac{1}{2003}\right)}{\left(1-\dfrac{1}{2}\right)\left(1+\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{100}\right)\left(1+\dfrac{1}{100}\right)}\)
\(=\dfrac{\dfrac{100}{101}\cdot\dfrac{101}{102}\cdot...\cdot\dfrac{2002}{2003}}{\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1+\dfrac{1}{100}\right)}\)
\(=\dfrac{100}{2003}:\left(\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{101}{100}\right)\)
\(=\dfrac{100}{2003}:\left(\dfrac{101}{2}\right)=\dfrac{100}{2003}\cdot\dfrac{2}{101}=\dfrac{200}{202303}\)
RL
3
31 tháng 12 2023
a: \(A=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{10}-1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-9}{10}\)
\(=-\dfrac{1}{10}\)
9<10
=>1/9>1/10
=>\(-\dfrac{1}{9}< -\dfrac{1}{10}\)
=>\(A>-\dfrac{1}{9}\)
b: \(B=\left(\dfrac{1}{4}-1\right)\left(\dfrac{1}{9}-1\right)\cdot...\cdot\left(\dfrac{1}{100}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{10}-1\right)\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{10}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-9}{10}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{11}{10}\)
\(=\dfrac{-1}{10}\cdot\dfrac{11}{2}=\dfrac{-11}{20}\)
20<21
=>\(\dfrac{11}{20}>\dfrac{11}{21}\)
=>\(-\dfrac{11}{20}< -\dfrac{11}{21}\)
=>\(B< -\dfrac{11}{21}\)
18 tháng 3 2017
a)
\(A=\dfrac{3}{4}.\dfrac{8}{9}...\dfrac{9999}{10000}\)
\(=\dfrac{1.3}{2.2}.\dfrac{2.4}{3.3}...\dfrac{99.101}{100.100}\)
\(=\dfrac{1.2...99}{2.3...100}.\dfrac{3.4...101}{2.3...100}\)
\(=\dfrac{1}{100}.\dfrac{101}{2}\)
\(=\dfrac{101}{200}\)
HT
15 tháng 5 2017
\(T=\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{5}\right)\left(1-\dfrac{1}{7}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{8}\right)\left(1-\dfrac{1}{10}\right)\)\(\Rightarrow T=\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}.\dfrac{8}{9}.\dfrac{10}{11}.\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.\dfrac{7}{8}.\dfrac{9}{10}\)
\(\Rightarrow=\dfrac{1}{11}\)
\(\Rightarrow\) Số nghịch đảo của T là \(11\)
7 tháng 3 2021
Sửa đề: \(B=\left(\dfrac{1}{4}-1\right)\left(\dfrac{1}{9}-1\right)\left(\dfrac{1}{16}-1\right)\cdot...\cdot\left(\dfrac{1}{400}-1\right)\)
Ta có: \(B=\left(\dfrac{1}{4}-1\right)\left(\dfrac{1}{9}-1\right)\left(\dfrac{1}{16}-1\right)\cdot...\cdot\left(\dfrac{1}{400}-1\right)\)
\(=\dfrac{-3}{4}\cdot\dfrac{-8}{9}\cdot\dfrac{-15}{16}\cdot...\cdot\dfrac{-399}{400}\)
\(=\dfrac{-3\cdot8\cdot15\cdot...\cdot399}{4\cdot9\cdot16\cdot...\cdot400}\)
\(=\dfrac{-3\cdot2\cdot4\cdot3\cdot5\cdot...\cdot19\cdot21}{2^2\cdot3^2\cdot4^2\cdot...\cdot20^2}\)
\(=\dfrac{-2\cdot3\cdot4\cdot...\cdot19}{2\cdot3\cdot4\cdot...\cdot20}\cdot\dfrac{3\cdot4\cdot5\cdot...\cdot21}{2\cdot3\cdot4\cdot20}\)
\(=\dfrac{-1}{20}\cdot\dfrac{21}{2}\)
\(=\dfrac{-21}{40}\)
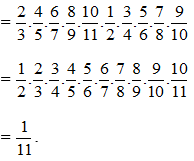
\(1-\dfrac{1}{n^2}=\dfrac{n^2-1}{n^2}=\dfrac{\left(n-1\right)\left(n+1\right)}{n^2}\)
\(\Rightarrow\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)...\left(1-\dfrac{1}{n^2}\right)=\dfrac{1.3.2.4...\left(n-1\right)\left(n+1\right)}{2^2.3^2...n^2}\)
\(=\dfrac{1.2...\left(n-1\right)}{2.3...n}.\dfrac{3.4...\left(n+1\right)}{2.3...n}=\dfrac{1}{n}.\dfrac{n+1}{2}=\dfrac{n+1}{2n}\)