Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


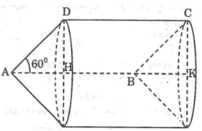
*Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón
Trong tam giác AHD,ta có:
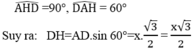
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
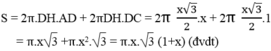
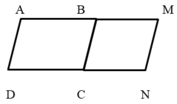
*Khi quay hình bình hành ABCD một vòng quanh AD thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AB = DC = 1, cạnh BC vạch nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón
Ta có:
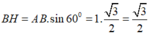
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
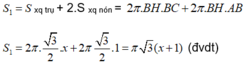

Kẻ DH ^ AB tại H
⇒ A H = A D 2 = 4 c m
Áp dụng định lý Pytago trong D vuông ADH Þ DH = 4 3 cm.
ÞSABCD = DH.AB = 120cm2

a) Xét tam giác vuông AMD và tam giác vuông CBN ta có :
\(\widehat{AMD}=\widehat{CNB}=90^o\) ( GT )
\(AD=CB\)( Vì ABCD là hình bình hành )
\(\widehat{ADM}=\widehat{CBN}=60^o\) ( góc đối của hình bình hành ABCD )
Do đó : \(\Delta AMD=\Delta CBN\)( cạnh huyền - góc nhọn )
\(\Rightarrow\hept{\begin{cases}AM=CN\\DM=NB\end{cases}}\)( các cặp cạnh tương ứng )
\(\Rightarrow\hept{\begin{cases}AM=CN\\AN=CM\end{cases}}\) ( vì AB=CD )
=> ANCM là hình bình hành
Xét hình bình hành ANCM ta có :
góc AMC=90 độ
=> AMCN là hình chữ nhật . ( dấu hiệu nhận biết 3 )
b) Ta có O là điểm giao hai đường chéo AC và BD của hình bình hành ABCD .
=> O là trung điểm của AC và BD . (1)
Và ANCM là hình bình hành ( câu a )
=> O là giao điểm của hai đường chéo AC và MN
=> O cũng là trung điểm của MN (2)
Từ (1) và (2)
=> AC , BD và MN đồng quy tại điểm O ( đpcm)

Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có :
BC = BM = MN = 3 cm
Chiều cao tương ứng cạnh DC của hình bình hành ABCD là :
8 : 4 = 2 (cm)
Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là :
3 x 2 = 6 (cm2)
Đáp số : 6 cm2
Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có :
BC = BM = MN = 3 cm
Chiều cao tương ứng cạnh DC của hình bình hành ABCD là :
8 : 4 = 2 (cm)
Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là :
3 x 2 = 6 (cm2) Đáp số:6 cm2