Bn nào giải nhanh giúp mik với mik đang cần gấp 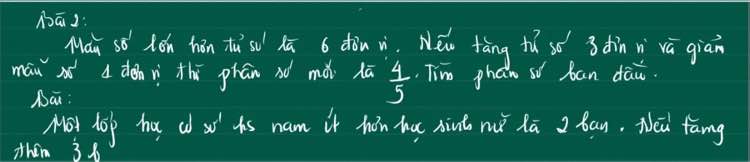
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: =>x+2022=0
hay x=-2022
b: \(\Leftrightarrow x-198=0\)
hay x=198

a: \(\Leftrightarrow\left(x+8-3x+7\right)\left(x+8+3x-7\right)=0\)
=>(-2x+15)(4x+1)=0
=>x=15/2 hoặc x=-1/4
b: \(\Leftrightarrow\left(x-5\right)\left(x+6-x+5\right)=0\)
=>x-5=0
hay x=5
c: \(\Leftrightarrow x^2+15x+56-x^2+6x-9=0\)
=>21x=-47
hay x=-47/21

Mình nhớ câu này mình đã giải rồi, không biết vì lý do gì mà bạn lại xóa đi vậy nhỉ? Và nếu CH đã đăng, yêu cầu bạn không đăng lại lần thứ 2!

\(f,=\left(5^2+3\right):7=28:7=4\\ g,=7^2-9+8\cdot25=49-9+200=240\\ h,=600+72+18=690\\ i,=5^2+5-20=10\\ j,=45-28+83=100\)

\(2A=\frac{4}{1.5}+\frac{6}{5.11}+\frac{8}{11.19}+\frac{10}{19.29}+\frac{12}{29.41}\)
\(=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{11}+\frac{1}{11}-\frac{1}{19}+...+\frac{1}{29}-\frac{1}{41}=1-\frac{1}{41}=\frac{40}{41}\)
\(\Rightarrow A=\frac{20}{21}\)
\(3B=\frac{3}{1.4}+\frac{6}{4.10}+\frac{9}{10.19}+\frac{12}{19.31}=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{10}+\frac{1}{10}-\frac{1}{19}+\frac{1}{19}-\frac{1}{31}\)
\(=1-\frac{1}{31}=\frac{30}{31}\)
\(\Rightarrow B=\frac{10}{31}=\frac{20}{62}<\frac{20}{41}\)
Do đó $A>B$
Ta có: \(A=\dfrac{2}{1.5}+\dfrac{3}{5.11}+\dfrac{4}{11.19}+\dfrac{5}{19.29}+\dfrac{6}{29.41}\)
\(2A=1-\dfrac{1}{5}+\dfrac{1}{5}+...+\dfrac{1}{29}-\dfrac{1}{41}\)
\(2A=1-\dfrac{1}{41}=\dfrac{40}{41}\)
\(A=\dfrac{20}{41}\)
Lại có: \(B=\dfrac{1}{1.4}+\dfrac{2}{4.10}+\dfrac{3}{10.19}+\dfrac{4}{19.31}\)
\(3B=\dfrac{3}{1.4}+\dfrac{6}{4.10}+\dfrac{9}{10.19}+\dfrac{12}{19.31}\)
\(3B=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{10}+...+\dfrac{1}{19}-\dfrac{1}{31}\)
\(3B=1-\dfrac{1}{31}=\dfrac{30}{31}\)
\(B=\dfrac{10}{31}\)
Vì \(\dfrac{20}{41}>\dfrac{10}{31}\) nên...

(3) \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\)
\(\Leftrightarrow\) \(\dfrac{a^2+b^2}{ab}\ge2\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\left(luôn đúng\right)\)
(4)\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{9}{a +b+c}\)
\(\Leftrightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\left(a+b+c\right)\ge9\)
\(\Leftrightarrow1+\dfrac{b}{a}+\dfrac{c}{a}+\dfrac{a}{b}+1+\dfrac{c}{b}+\dfrac{a}{c}+\dfrac{b}{c}+1\ge9\)
\(\Leftrightarrow3+\left(\dfrac{a}{b}+\dfrac{b}{a}\right)+\left(\dfrac{b}{c}+\dfrac{c}{b}\right)+\left(\dfrac{a}{c}+\dfrac{c}{a}\right)\ge3+2+2+2\ge9\) (đpcm)

gọi d là ƯCLN(18n+3,21n+7)
ta có 18n+3chia hết cho d
21n+7 chia hết cho d
⇔21n+7-18n-3 chia hết cho d
⇔126n+42-126n-21 chia hết cho d
21 chia hết cho d
⇒d∈Ư(21)=1;3;7;21
n ≠ 3k-1;3k-3;3k-7;3k-21
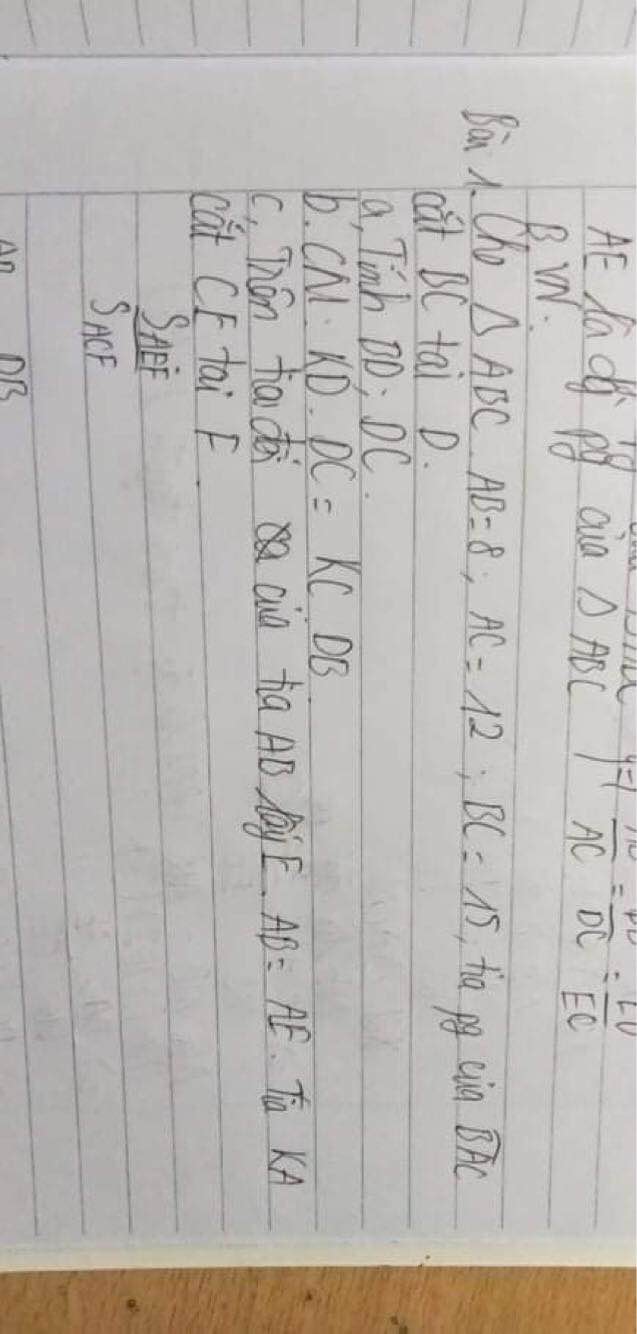

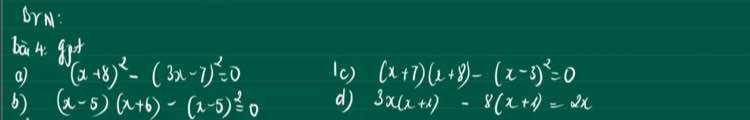



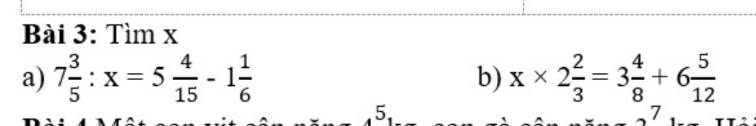
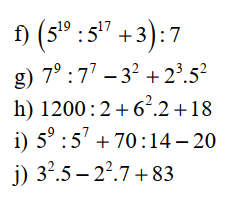 giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim
giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim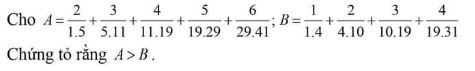
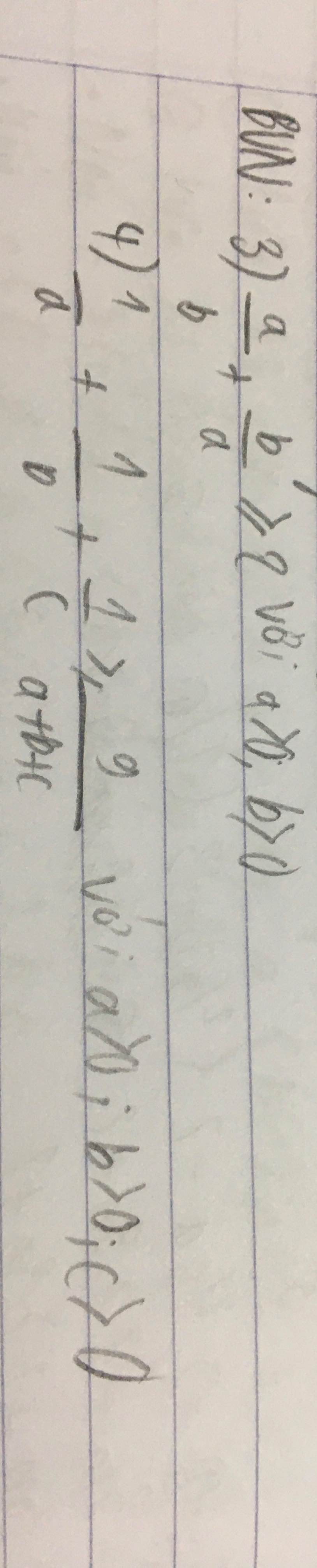


Bài 2:
Gọi tử là x
Mẫu là x+6
Theo đề, ta có:
\(\dfrac{x+3}{x+5}=\dfrac{4}{5}\)
=>5x+15=4x+20
=>x=5