Tìm các số nguyên p, q sao cho đa thức x4 + px2 + q chia hết cho đa thức x2 + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 5 2023
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
10 tháng 5 2023
\(\dfrac{2x^5+x^4+3x^3-4x^2-14x+m+1}{x^2-2}\)
\(=\dfrac{2x^5-4x^3+x^4-2x^2+7x^3-14x-2x^2+4+m-3}{x^2-2}\)
\(=2x^2+x^2+7x-2+\dfrac{m-3}{x^2-2}\)
Đây là phép chia hết khi m-3=0
=>m=3
26 tháng 12 2021
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
19 tháng 9 2023
a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
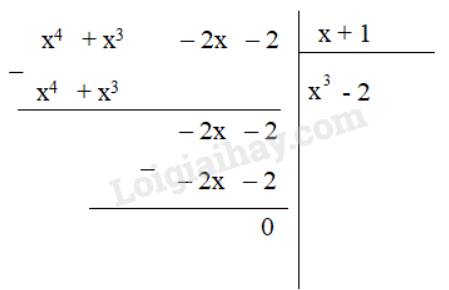
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
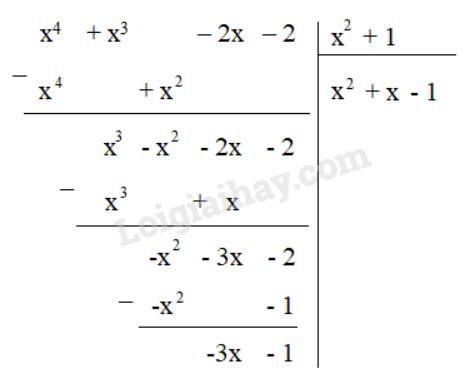
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn
23 tháng 12 2021
Đặt \(f\left(x\right)=2x^3-3x^2+x+a\)
Ta có: phép chia \(f\left(x\right)\) cho \(x+2\) có dư là \(R=f\left(-2\right)\)
\(\Rightarrow f\left(-2\right)=2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a\)
\(f\left(-2\right)=2.\left(-8\right)-3.4-2+a\)
\(f\left(-2\right)=-16-12-2+a\)
\(f\left(-2\right)=-20+a\)
Để \(f\left(x\right)\) chia hết cho \(x+2\) thì \(R=0\) hay \(f\left(-2\right)=0\)
\(\Rightarrow-20+a=0\Leftrightarrow a=20\)
CM
31 tháng 10 2019
Thu gọn Q(x) = x4 + 7x2 + 1
Khi đó R(x) = Q(x) - P(x) = 4x2 + 3x + 2. Chọn A
18 tháng 3 2022
a. cậu thu gọn bằng cách dùng t/c kết hợp và giao hoán
b. cậu thay từng giá vào biểu thức vừa được rút gọn để tìm
c. thì.... tớ ko biết
26 tháng 1 2024
\(x^4+x^3-2x^2+x+a⋮x+1\)
=>\(x^4+x^3-2x^2-2x+3x+3+a-3⋮x+1\)
=>a-3=0
=>a=3
\(x^4+px^2+q=\left(x^4+x^2\right)+\left(p-1\right)x^2+p-1+1-p+q\)
\(=\left(x^2+1\right)\left(x^2+p-1\right)+1-p+q\)
Để thỏa đề bài thì:
\(q+1-p=0\)
\(\Leftrightarrow q=p-1\)