giup mik voiiiiii...
Đọc tiếp
giup mik voiiiiii gap
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
16 tháng 12 2023
a: x-1 là bội của x+2
=>\(x-1⋮x+2\)
=>\(x+2-3⋮x+2\)
=>\(-3⋮x+2\)
=>\(x+2\inƯ\left(-3\right)\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)
b: 3x+1 là ước của x+2
=>\(x+2⋮3x+1\)
=>\(3x+6⋮3x+1\)
=>\(3x+1+5⋮3x+1\)
=>\(5⋮3x+1\)
=>\(3x+1\in\left\{1;-1;5;-5\right\}\)
=>\(3x\in\left\{0;-2;4;-6\right\}\)
=>\(x\in\left\{0;-\dfrac{2}{3};\dfrac{4}{3};-2\right\}\)
mà x nguyên
nên \(x\in\left\{0;-2\right\}\)
c: x+3 là ước của 2x+1
=>\(2x+1⋮x+3\)
=>\(2x+6-7⋮x+3\)
=>\(-7⋮x+3\)
=>\(x+3\in\left\{1;-1;7;-7\right\}\)
=>\(x\in\left\{-2;-4;4;-10\right\}\)
d: 3x+2 là bội của 2x-1
=>\(3x+2⋮2x-1\)
=>\(6x+4⋮2x-1\)
=>\(6x-3+7⋮2x-1\)
=>\(7⋮2x-1\)
=>\(2x-1\in\left\{1;-1;7;-7\right\}\)
=>\(2x\in\left\{2;0;8;-6\right\}\)
=>\(x\in\left\{1;0;4;-3\right\}\)
TN
0
N
0
H
3
13 tháng 8 2023
\(...=1+1+...+1+1\)
Số số 1 là :
\(\left(2022-2\right):2+1+1=1012\left(số\right)\)
Vậy kết quả là \(1x1012=1012\)
NT
Nguyễn Thị Nga
VIP
13 tháng 8 2023
Số số 1 là :
(2022−2):2+1+1=1012(��^ˊ)(2022−2):2+1+1=1012(sốo^ˊ)
Vậy kết quả là 1�1012=10121x1012=1012
P
1
TM
25 tháng 8 2023
Bài 1. (a) Điều kiện: \(x\ne\pm1\).
Ta có: \(A=\left(\dfrac{x-2}{x-1}-\dfrac{x+3}{x+1}+\dfrac{3}{x-1}\right):\left(1-\dfrac{x+3}{x+1}\right)\)
\(=\left(\dfrac{x-2+3}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-\left(x+3\right)}{x+1}\)
\(=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-x-3}{x+1}\)
\(=\dfrac{\left(x+1\right)^2-\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}:\dfrac{-2}{x+1}\)
\(=\dfrac{x^2+2x+1-x^2-2x+3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}\)
\(=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}=\dfrac{2}{1-x}\)
Vậy: \(A=\dfrac{2}{1-x}\)
(b) \(A=3\Leftrightarrow\dfrac{2}{1-x}=3\)
\(\Rightarrow1-x=\dfrac{2}{3}\Leftrightarrow x=\dfrac{1}{3}\left(TM\right)\)
Vậy: \(x=\dfrac{1}{3}\)
Bài 2. (a) Phương trình tương đương với:
\(\dfrac{3\left(3x-2\right)}{12}+\dfrac{6\left(x+3\right)}{12}=\dfrac{4\left(x-1\right)}{12}+\dfrac{x+1}{12}\)
\(\Rightarrow3\left(3x-2\right)+6\left(x+3\right)=4\left(x-1\right)+x+1\)
\(\Leftrightarrow9x-6+6x+18=4x-4+x+1\)
\(\Leftrightarrow10x=-15\Leftrightarrow x=-\dfrac{3}{2}\)
Vậy: Phương trình có tập nghiệm \(S=\left\{-\dfrac{3}{2}\right\}\).
(b) Điều kiện: \(x\ne\pm1\). Phương trình tương đương với:
\(\dfrac{2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{2x^2+2}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow2\left(x+1\right)+2\left(x-1\right)=2x^2+2\)
\(\Leftrightarrow2x+2+2x-2=2x^2+2\)
\(\Leftrightarrow2x^2-4x+2=0\Leftrightarrow2\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow2\left(x-1\right)^2=0\Rightarrow x-1=0\Leftrightarrow x=1\left(KTM\right)\)
Vậy: Phương trình có tập nghiệm \(S=\varnothing\)
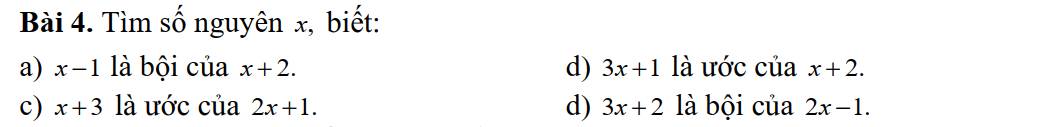
Gọi số cần tìm là \(\overline{ab}\) theo đề bài ta có
\(a+b=8\left(1\right)\)
Ta có
\(\overline{ba}-\overline{ab}=18\Rightarrow10b+a-10a-b=18\)
\(\Leftrightarrow b-a=2\left(2\right)\)
Giải hệ \(\hept{\begin{cases}a+b=8\\b-a=2\end{cases}\Rightarrow\hept{\begin{cases}a=3\\b=5\end{cases}}}\)
Số cần tìm là 35