Cho một lục giác nội tiếp, khi đó đường thẳng nối tâm của các đường tròn ngoại tiếp của các tam giác đối diện mà các tam giác này tạo bởi một cạnh của lục giác và giao điểm của đường thẳng kéo dài của hai cạnh liền kề của lục giác đó sẽ đồng quy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 10 2017
a, Giả sử ∆ABC vuông tại A. Gọi O là trung điểm của BC
=> OA = OB = OC => O là tâm đường tròn đi qua A,B,C
b, Ta có OA = OB = OC => OA = 1 2 BC => ∆ABC vuông tại A
19 tháng 6 2019
a) Ta có ^AIC' = ^IAC + ^ICA = ^IAB + ^ICB = ^IAB + ^BAC' = ^IAC' => \(\Delta\)AC'I cân tại C'
=> C' nằm trên trung trực của AI. Tương tự B' cũng nằm trên trung trực của AI => B'C' vuông góc AI
Hay A'I vuông góc với B'C'. Lập luận tương tự B'I vuông góc A'C', C'I vuông góc A'B'
Do đó I là trực tâm của \(\Delta\)A'B'C' (đpcm).
b) Ta thấy ^FDE = ^A'DC' = ^A'AC' = ^IAC' = C'IA (Vì \(\Delta\)AC'I cân tại C') = ^EIC'
Suy ra tứ giác DEIF nội tiếp (đpcm).
c) Gọi S là tâm ngoại tiếp của \(\Delta\)DEF. Vì tứ giác DEIF nội tiếp (cmt) nên S đồng thời là tâm ngoại tiếp DEIF
Gọi giao điểm thứ hai giữa (S) và (O) là G. Khi đó ^DFG = ^DEG => ^GFA' = ^GEC'
Lại có ^EGF = ^EDF = ^A'DC' = ^A'GC' => ^FGA' = ^EGC'. Do vậy \(\Delta\)GEC' ~ \(\Delta\)GFA' (g.g)
=> \(\frac{GC'}{GA'}=\frac{EC'}{FA'}\). Mặt khác ^A'IF = ^C'IA = ^C'AI = ^C'AE và ^IA'F = ^AA'D = ^AC'D = ^AC'E
Cho nên \(\Delta\)AEC' ~ \(\Delta\)IFA' (g.g) => \(\frac{EC'}{FA'}=\frac{AC'}{IA'}\). Mà các điểm A,I,A',C' đều cố định
Nên tỉ số \(\frac{AC'}{FA'}\) là bất biến. Như vậy \(\frac{GC'}{GA'}\)không đổi, khi đó tỉ số giữa (GC' và (GA' của (O) không đổi
Kết hợp với (O), A',C' cố định suy ra G là điểm cố định. Theo đó trung trực của IG cố định
Mà S thuộc trung trực của IG (do D,I,E,F,G cùng thuộc (S)) nên S di động trên trung trực của IG cố định (đpcm).
CM
24 tháng 3 2019
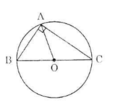
Hình a) + b)
a) Xét tam giác ABC vuông tại A. Gọi O là trung điểm của BC.
Ta có AO là đường trung tuyến ứng với cạnh huyền nên OA = OB = OC.
=> O là tâm của đường tròn đi qua A, B, C.
Vậy tâm của đường tròn ngoại tiếp ΔABC là trung điểm của cạnh huyền BC. (đpcm)
b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC, ta có:
OA = OB = OC
Tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC nên suy ra tam giác ABC vuông tại A. (đpcm)