Cho tam giác ABC, trung tuyến AM cắt phân giác CD tại I.cm IC/ID - BC/AC =1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 3 2023
a: Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
BA=BD
=>ΔBAH=ΔBDH
=>góc ABH=góc DBH
=>BH là phân giác của góc ABD
b: ΔABC vuông tại A
mà AM là trung tuyến
nên MA=MB
=>ΔMAB cân tại M
13 tháng 4 2019
a ) Xét ∆BAD và ∆CAD
AB = AC ( ∆ABC cân )
\(\widehat{B}=\widehat{C}\)
\(\widehat{BAD}=\widehat{DAC}\)
=> ∆ABH = ∆ACH(g.c.g)
AH
Akai Haruma
Giáo viên
13 tháng 1 2024
Lời giải:
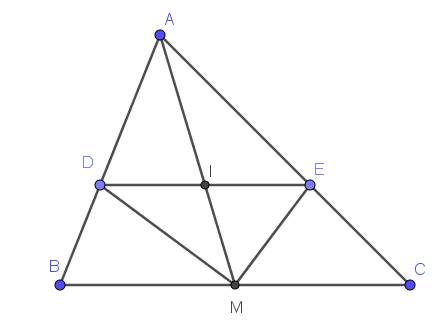
a. Áp dụng tính chất tia phân giác đối với tam giác $AMB, AMC$ thì:
$\frac{AD}{DB}=\frac{AM}{MB}$
$\frac{AE}{EC}=\frac{AM}{MC}$
Mà $MB=MC$ (do $M$ là trung điểm $BC$)
$\Rightarrow \frac{AD}{DB}=\frac{AE}{EC}$
$\Rightarrow DE\parallel BC$ (theo định lý Talet đảo)
b.
Tam giác $ABM$ có $DI\parallel BM$ (do $DE\parallel BC$) nên áp dụng định lý Talet:
$\frac{DI}{BM}=\frac{AI}{AM}$
Tam giác $ACM$ có $IE\parallel CM$ (do $DE\parallel BC$) nên áp dụng định lý Talet:
$\frac{IE}{MC}=\frac{AI}{AM}$
$\Rightarrow \frac{DI}{BM}=\frac{IE}{MC}$
Mà $BM=CM$ nên $DI=IE$
$\Rightarrow I$ là trung điểm $DE$>
ccccc đụ má