cho hình thang abcd và ac cắt bd tại i. đường thẳng qua i và song song với hai đáy cắt ad và bc lần lượt ở m và n. chứng minh a, mi/ab=cn/cb b, mi=in
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2020
https://h.vn/hoi-dap/tim-kiem?q=cho+h%C3%ACnh+thang+ABCD+%28AB%2F%2FCD%29.+C%C3%B3+AC+c%E1%BA%AFt+BD+t%E1%BA%A1i+I.+%C4%90%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+qua+I+v%C3%A0+song+song+c%E1%BB%9Bi+hai+%C4%91%C3%A1y+c%E1%BA%AFt+AD+v%C3%A0+BC+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+%E1%BB%9F+M+v%C3%A0+N.+Ch%E1%BB%A9ng+Minh+%3A+1%29+MI%2FAB+%3DCN%2FCB+.+2%29+MI%3DIN&subject=0
k bt lm nhờ mạng giải giùm nên thông cảm cho nha ng ae
CH
Cô Hoàng Huyền
Admin
VIP
22 tháng 3 2018
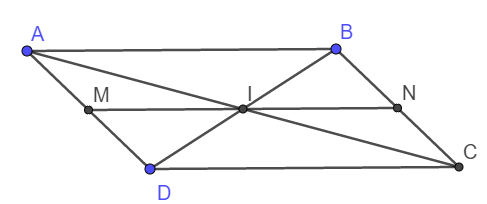
1. Xét tam giác ABD có MI // AB nên theo định lý Talet ta có:
\(\frac{MI}{AB}=\frac{DI}{DB}\)
Xét tam giác ABC có NI // AB nên theo định lý Talet ta có:
\(\frac{NI}{AB}=\frac{NC}{BC}\)
2. Xét tam giác BDC có IN // DC nên \(\frac{DI}{DB}=\frac{NC}{BC}\)
Từ đó ta có: \(\frac{MI}{AB}=\frac{NI}{AB}\Rightarrow MI=IN\)
Vậy I là trung điểm MN (đpcm)
30 tháng 6 2023
a: Xét ΔIAB và ΔICD có
góc IAB=góc ICD
góc AIB=góc CID
=>ΔIAB đồng dạng với ΔICD
=>IA/IC=IB/ID
=>AI/AC=BI/BD
b: Xét ΔADC có MI//DC
nên MI/DC=AI/AC
Xét ΔBDC có NI//DC
nên NI/DC=BI/BD
=>MI/DC=NI/DC
=>MI=NI
31 tháng 8 2019
a) Ta có:
+) M là trung điểm của AD và MN // CD
MN là đường trung bình của hình thang ABCD
N là trung điểm của BC
+) M là trung điểm của AB và ME // AB
ME là đường trung...
28 tháng 9 2019
Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC
ai la nguoi yeu cua toi