Lập phương trình mặt cầu (S), biết S đi qua C (2; -4; 3) và đi qua các hình chiếu của C lên
a) 3 trục toạ độ
b) 3 mặt phẳng toạ độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình mặt cầu ở đáp án (C) có tâm I ( 3;3;-3 ) và bán kính R = 3 nên R = x 1 = y 1 = z 1 .
Do đó (S) tiếp xúc với ba mặt phẳng tọa độ. Hơn nữa M thỏa mãn phương trình (S) nên M ∈ S
Đáp án C

Đáp án D
Phương trình tổng quát của mặt cầu (S) có dạng x 2 + y 2 + z 2 - 2ax - 2by - 2cz + d = 0 với a 2 + b 2 + c 2 - d > 0
Ta có: O(0; 0; 0) ∈ (S) ⇔ d = 0
A(-4; 0; 0) ∈ (S) ⇔ ( - 4 ) 2 + 0 2 + 0 2 - 2a.(-4) - 0 - 0 + 0 = 0 ⇔ a = -2
B(0; 2; 0) ∈ (S) ⇔ 0 2 + 2 2 + 0 2 - 0 - 2b.2 - 0 + 0 = 0 ⇔ b = 1
C(0; 0; 4) ∈ (S) ⇔ 0 2 + 0 2 + 4 2 - 0 - 0 - 2c.4 - 0 = 0 ⇔ c = 2
Vậy phương trình tổng quát của mặt cầu (S) là: x 2 + y 2 + z 2 + 4x -2y - 4z = 0

Đáp án A
Gọi I(a,b,c) là tâm của mặt cầu (S). Ta có:
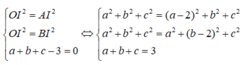
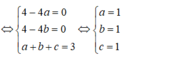
=> I(1; 1; 1); R = OI = 3
Vậy phương trình của mặt cầu (S) là: ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 3

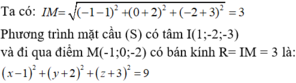

Gọi I(a;b;c) và r lần lượt là tâm và bán kính mặt cầu (S).
Phương trình mặt cầu (S) có dạng: (x-a)2+(y-b)2+(z-c)2=r2.
a) (S) đi qua các điểm C(2;-4;3), (2;0;0), (0;-4;0) và (0;0;3).
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\left(2-a\right)^2+\left(-4-b\right)^2+\left(3-c\right)^2=r^2\\\left(2-a\right)^2+b^2+c^2=r^2\\a^2+\left(-4-b\right)^2+c^2=r^2\\a^2+b^2+\left(3-c\right)^2=r^2\end{matrix}\right.\) \(\Rightarrow\) a=1, b=-2, c=3/2, r2=29/4.
Phương trình cần tìm là: (S): (x-1)2+(y+2)2+(z-3/2)2=29/4.
b) (S) đi qua các điểm C(2;-4;3), (2;-4;0), (2;0;3) và (0;-4;3).
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\left(2-a\right)^2+\left(-4-b\right)^2+\left(3-c\right)^2=r^2\\\left(2-a\right)^2+\left(-4-b\right)^2+c^2=r^2\\a^2+\left(-4-b\right)^2+\left(3-c\right)^2=r^2\\\left(2-a\right)^2+b^2+\left(3-c\right)^2=r^2\end{matrix}\right.\) \(\Rightarrow\) a=1, b=-2, c=3/2, r2=29/4.
Phương trình cần tìm là: (S): (x-1)2+(y+2)2+(z-3/2)2=29/4.