Tìm x:(x-5).(2x-1)=3x(x-5)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(6x\left(x-5\right)+3x\left(7-2x\right)=18\)
\(\Leftrightarrow6x^2-30x+21x-6x^2=18\)
\(\Leftrightarrow-9x=18\)
hay x=-2
Vậy: S={-2}
b) Ta có: \(2x\left(3x+1\right)+\left(4-2x\right)\cdot3x=7\)
\(\Leftrightarrow6x^2+2x+12x-6x^2=7\)
\(\Leftrightarrow14x=7\)
hay \(x=\dfrac{1}{2}\)
Vậy: \(S=\left\{\dfrac{1}{2}\right\}\)
c) Ta có: \(0.5x\left(0.4-4x\right)+\left(2x+5\right)\cdot x=-6.5\)
\(\Leftrightarrow0.2x-2x^2+2x^2+5x=-6.5\)
\(\Leftrightarrow5.2x=-6.5\)
hay \(x=-\dfrac{5}{4}\)
Vậy: \(S=\left\{-\dfrac{5}{4}\right\}\)
d) Ta có: \(\left(x+3\right)\left(x+2\right)-\left(x-2\right)\left(x+5\right)=6\)
\(\Leftrightarrow x^2+5x+6-\left(x^2+3x-10\right)=6\)
\(\Leftrightarrow x^2+5x+6-x^2-3x+10=6\)
\(\Leftrightarrow2x+16=6\)
\(\Leftrightarrow2x=-10\)
hay x=-5
Vậy: S={-5}
e) Ta có: \(3\left(2x-1\right)\left(3x-1\right)-\left(2x-3\right)\left(9x-1\right)=0\)
\(\Leftrightarrow3\left(6x^2-5x+1\right)-\left(18x^2-29x+3\right)=0\)
\(\Leftrightarrow18x^2-15x+3-18x^2+29x-3=0\)
\(\Leftrightarrow14x=0\)
hay x=0
Vậy: S={0}


a: Ta có: \(x\left(2x-3\right)-\left(2x-1\right)\left(x+5\right)=17\)
\(\Leftrightarrow2x^2-3x-2x^2-10x+x+5=17\)
\(\Leftrightarrow-12x=12\)
hay x=-1

a) 3x(4x-3)-2x(5-6x)=0
\(\Leftrightarrow12x^2-9x-10x+12x^2=0\)
\(\Leftrightarrow24x^2-19x=0\)
\(\Leftrightarrow x\left(24x-19\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\24x-19=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\24x=19\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{19}{24}\end{matrix}\right.\)
Vậy x=0 hoặc x=\(\dfrac{19}{24}\)

a: Ta có: \(3\left(2x-3\right)+2\left(2-x\right)=-3\)
\(\Leftrightarrow6x-9+4-2x=-3\)
\(\Leftrightarrow4x=2\)
hay \(x=\dfrac{1}{2}\)

a) \(\left|2x-5\right|=x+1\)
<=> \(\orbr{\begin{cases}2x-5=x+1\left(x\ge\frac{5}{2}\right)\\5-2x=x+1\left(x< \frac{5}{2}\right)\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-6\left(ktm\right)\\3x=4\end{cases}}\)
<=> \(x=\frac{4}{3}\left(tm\right)\)
b) \(\left|3x-2\right|-1=2x\) <=> \(\left|3x-2\right|=2x+1\)
<=> \(\orbr{\begin{cases}3x-2=2x+1\left(x\ge\frac{2}{3}\right)\\2-3x=2x+1\left(x< \frac{2}{3}\right)\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-3\left(ktm\right)\\5x=1\end{cases}}\) <=> \(x=\frac{1}{5}\left(tm\right)\)
c) \(\left|x-5\right|+5=x\) <=> \(\left|x-5\right|=x-5\)
<=> \(\orbr{\begin{cases}x-5=x-5\left(x\ge5\right)\\5-x=x-5\left(x< 5\right)\end{cases}}\)
<=> \(\orbr{\begin{cases}0x=0\\2x=10\end{cases}}\) <=> 0x = 0 (luôn đúng) hoặc x = 5 (ktm)
Vậy x \(\ge\)5
d) \(\left|3x-5\right|=3x-5\) <=> \(\orbr{\begin{cases}3x-5=3x-5\left(x\ge\frac{5}{3}\right)\\5-3x=3x-5\left(x< \frac{5}{3}\right)\end{cases}}\)
<=> \(\orbr{\begin{cases}0x=0\left(luônđúng\right)\\6x=10\end{cases}}\)
<=> \(\orbr{\begin{cases}x\ge\frac{5}{3}\\x=\frac{5}{3}\left(ktm\right)\end{cases}}\)Vậy x \(\ge\)5/3

a,6x-3-5x+15+18x-24=24
19x-12=24
19x=36
x=36/19
c,10x-6x2+6x2-10x+21=3
0x=-18
không có x
d,3x2+3x-2x2-4x=-1-x
x2-x=-1-x
x2-x+x=-1
x2=-1
không có x thỏa mãn

2:
a: =>x^2+3x-4x-12-(x^2-5x+x-5)=8
=>x^2-x-12-x^2+4x+5=8
=>3x-7=8
=>3x=15
=>x=5
b: =>3x^2+3x-2x-2-3x^2-21x=13
=>-20x=15
=>x=-3/4
c: =>x^2-25-x^2-2x=9
=>-2x=25+9=34
=>x=-17
d: =>x^3-1-x^3+3x=1
=>3x-1=1
=>3x=2
=>x=2/3

(x+2)(x+3)-(x-2)(x+5)=0
=> x2+5x+6-x2-3x+10=0
=>2x+16=0
=>2x=-16
=>x=-8
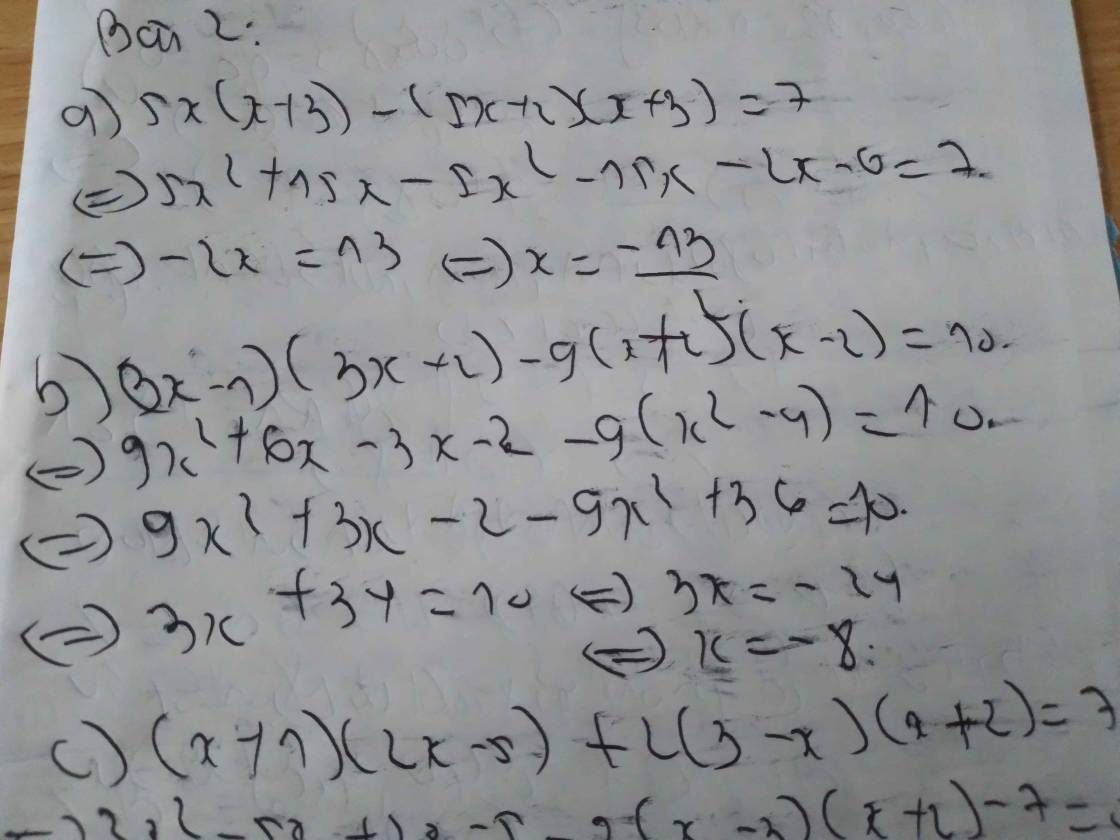


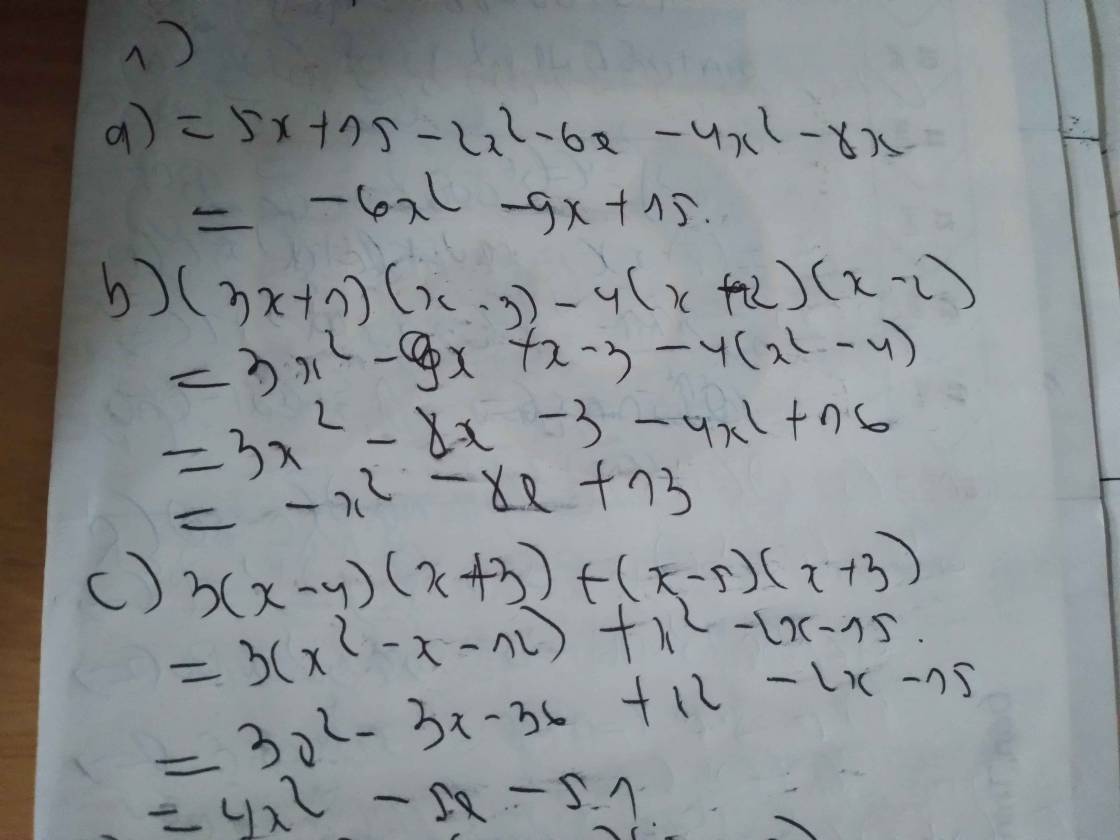
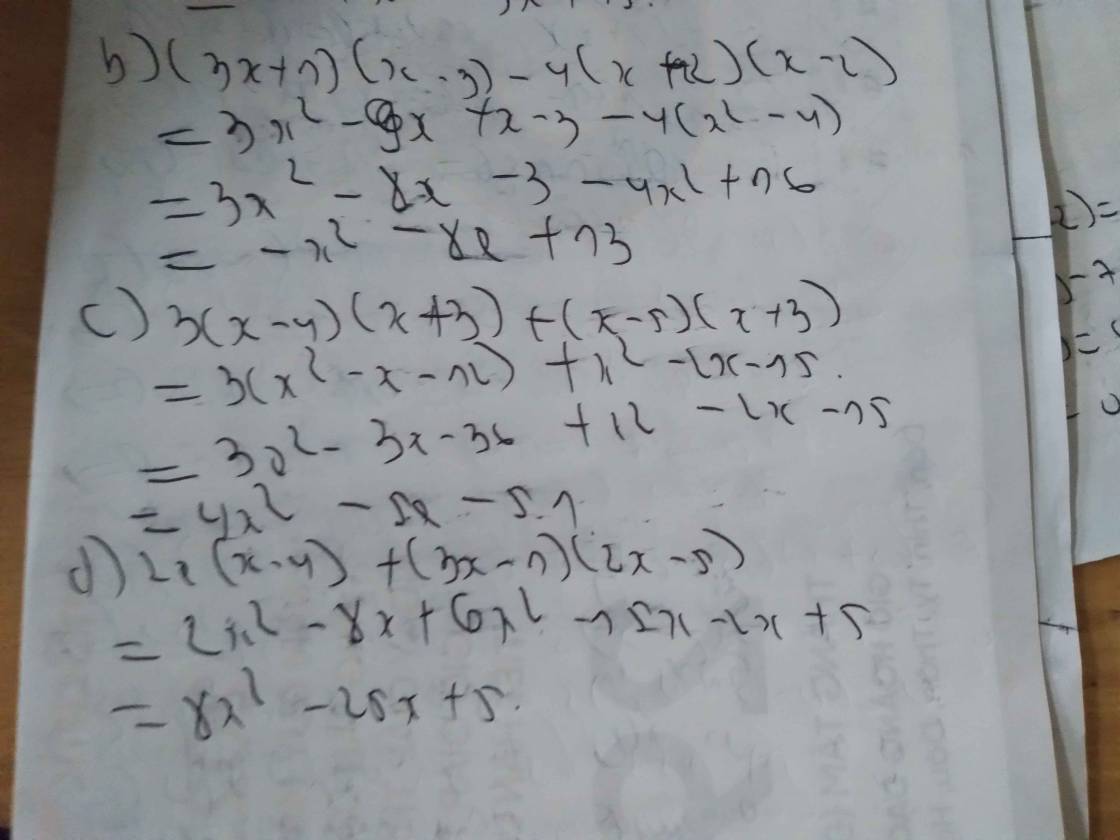
Answer:
\(\left(x-5\right)\left(2x-1\right)=3x\left(x-5\right)\)
\(\Rightarrow\left(x-5\right)\left(2x-1\right)-3x\left(x-5\right)=0\)
\(\Rightarrow\left(x-5\right)\left(2x-1-3x\right)=0\)
\(\Rightarrow\left(x-5\right)\left(-x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-5=0\\-x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=5\\-x=1\end{cases}}\Rightarrow\orbr{\begin{cases}x=5\\x=-1\end{cases}}\)