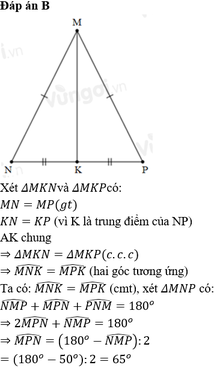
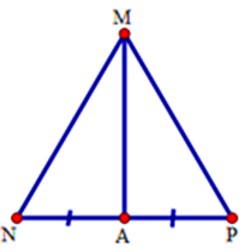
Cho tam giác MNP có MD là tia phân giác của NMP (với D thuộc NP) biết MDN là 85^0 . Khi đó MNP-MPN băng bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 1 2022
a: Xét ΔMNP có \(\widehat{N}=\widehat{P}\)
nên ΔMNP cân tại M
hay MN=MP
b: Ta có: ΔMNP cân tại M
mà MD là đường cao
nên MD là đường phân giác
10 tháng 5 2022
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
Do đó: ΔHNM\(\sim\)ΔMNP
b: \(NP=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(MH=\dfrac{MN\cdot MP}{NP}=4.8\left(cm\right)\)
\(HN=\dfrac{MN^2}{NP}=3.6\left(cm\right)\)
=>HP=6,4(cm)
JK
26 tháng 6 2020
a. xét tg MND và tg MPD có : MD chung
^PMD = ^NMD do MD là pg của ^PMN (Gt)
MN = MP do tg MNP cân tại M (gt)
=> tg MND = tg MPD (c-g-c)
b. tg MNP cân tại A (gt) có MD là pg
=> MD đồng thời là đường cao (đl) và là trung tuyến => DN = 6
=> tg MND vuông tại D (Đn)
=> MN^2 = MD^2 + DN^2 (đl Pytago)
DN = 6; MN =10
=> MD = 8 do MD > 0
c.
UT
18 tháng 4 2021
tự vẽ hình nhé
a, Xét \(\Delta\) MNP và \(\Delta\) HNM
< MNP chung
<NMP=<NHM(=90\(^0\) )
b,=> \(\dfrac{MN}{HN}=\dfrac{NP}{MN}\)
=> \(MN^2=NP\cdot NH\)
c, xét \(\Delta\) NMP vg tại M, áp dụng định lí Py - ta - go trong tam giác vg có
\(MN^2+MP^2=NP^2\)
=> \(NP^2=144\Rightarrow NP=12cm\)
Ta có \(MN^2=NH\cdot NP\)
Thay số:\(7,2^2=NH\cdot12\Rightarrow NH=4,32cm\)