Rút gọn biểu thức A = (1+1/3).(1+1/8).(1+1/15).....(1+1/2499)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 1
\(A=\left(1+\dfrac{1}{3}\right)\cdot\left(1+\dfrac{1}{8}\right)\left(1+\dfrac{1}{15}\right)\cdot...\left(1+\dfrac{1}{2499}\right)\)
\(=\dfrac{4}{3}\cdot\dfrac{9}{8}\cdot...\cdot\dfrac{2500}{2499}\)
\(=\dfrac{2\cdot2}{1\cdot3}\cdot\dfrac{3\cdot3}{2\cdot4}\cdot...\cdot\dfrac{50\cdot50}{49\cdot51}\)
\(=\dfrac{2\cdot3\cdot4\cdot...\cdot50}{1\cdot2\cdot3\cdot...\cdot49}\cdot\dfrac{2\cdot3\cdot...\cdot50}{3\cdot4\cdot...\cdot51}\)
\(=\dfrac{50}{1}\cdot\dfrac{2}{51}=\dfrac{100}{51}\)
NN
2
5 tháng 2 2022
A = \(\left(1+\frac{1}{3}\right)\left(1+\frac{1}{8}\right)\left(1+\frac{1}{15}\right)\)\(...\left(1+\frac{1}{2499}\right)\)
A = \(\left(\frac{3}{3}+\frac{1}{3}\right)\left(\frac{8}{8}+\frac{1}{8}\right)\left(\frac{15}{15}+\frac{1}{15}\right)\)\(...\left(\frac{2499}{2499}+\frac{1}{2499}\right)\)
A = \(\frac{4}{3}.\frac{9}{8}.\frac{16}{15}.....\frac{2500}{2499}\)
A = \(\frac{4.9.16.....2500}{3.8.15.....2499}\)
A = \(\frac{\left(2.2\right)\left(3.3\right)\left(4.4\right)...\left(50.50\right)}{3.8.15.24.....2499}\)
A = \(\frac{2.3.4.....50}{3.4.5.6.....51}\)
A = \(\frac{2}{51}\)
Vậy A = \(\frac{2}{51}\)
( Nếu sai mong bạn thông cảm ạ ! )
_HT_
YN
5 tháng 2 2022
Answer:
\(A=\left(1+\frac{1}{3}\right)\left(1+\frac{1}{8}\right)\left(1+\frac{1}{15}\right)...\left(1+\frac{1}{2499}\right)\)
\(=\frac{4}{3}.\frac{9}{8}.\frac{16}{15}...\frac{2500}{2499}\)
\(=\frac{2^2}{1.3}.\frac{3^2}{2.4}.\frac{4^2}{3.5}...\frac{50^2}{49.51}\)
\(=\frac{2^2.3^2.4^2...50^2}{1.3.2.4.3.5...49.51}\)
\(=\frac{2.50}{51}\)
\(=\frac{100}{51}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 4 2023
A = 1 + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\) +.......+\(\dfrac{1}{3^{n-1}}\) + \(\dfrac{1}{3^n}\)
3\(\times\) A = 3 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\)+........+ \(\dfrac{1}{3^{n-1}}\)
3A - A = 3 + \(\dfrac{1}{3}\) - 1 - \(\dfrac{1}{3^n}\)
2A = \(\dfrac{7}{3}\) - \(\dfrac{1}{3^n}\)
A = ( \(\dfrac{7}{3}\) - \(\dfrac{1}{3^n}\)): 2
A = \(\dfrac{7.3^{n-1}-1}{3^n}\) : 2
A = \(\dfrac{7.3^{n-1}-1}{2.3^n}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 4 2023
B = \(\dfrac{1}{2}\) - \(\dfrac{1}{2^2}\) + \(\dfrac{1}{2^3}\) - \(\dfrac{1}{2^4}\)+......+\(\dfrac{1}{2^{99}}\) - \(\dfrac{1}{2^{100}}\)
2B = 2 - \(\dfrac{1}{2}\) + \(\dfrac{1}{2^2}\) - \(\dfrac{1}{2^3}\)+ \(\dfrac{1}{2^4}\)-.......-\(\dfrac{1}{2^{99}}\)
2B + B = 2 - \(\dfrac{1}{2^{100}}\)
3B = 2 - \(\dfrac{1}{2^{100}}\)
B = ( 2 - \(\dfrac{1}{2^{100}}\)): 3
B = \(\dfrac{2.2^{100}-1}{2^{100}}\) : 3
B = \(\dfrac{2^{101}-1}{3.2^{100}}\)
PT
1
11 tháng 9 2016
\(A=\left(1+\frac{1}{3}\right).\left(1+\frac{1}{8}\right).\left(1+\frac{1}{15}\right)...\left(1+\frac{1}{n^2+2n}\right)\)
\(A=\frac{3+1}{3}.\frac{8+1}{8}.\frac{15+1}{15}...\frac{n^2+2n+1}{n^2+2n}\)
\(A=\frac{4}{3}.\frac{9}{8}.\frac{16}{15}...\frac{\left(n+1\right)^2}{n^2+2n}\)
\(A=\frac{2.2}{1.3}.\frac{3.3}{2.4}.\frac{4.4}{3.5}...\frac{\left(n+1\right)^2}{n.\left(n+2\right)}\)
\(A=\frac{2.3.4...\left(n+1\right)}{1.2.3...n}.\frac{2.3.4...\left(n+1\right)}{3.4.5...\left(n+2\right)}\)
\(A=\left(n+1\right).\frac{2}{n+2}=\frac{2.\left(n+1\right)}{n+2}\)
11 tháng 9 2016
Ta có : \(1+\frac{1}{k^2+2k}=\frac{k^2+2k+1}{k^2+2k}=\frac{\left(k+1\right)^2}{k\left(k+2\right)}\) với k thuộc N*
Áp dụng với k = 1,2,3,....,n được :
\(A=\left(1+\frac{1}{3}\right)\left(1+\frac{1}{8}\right)\left(1+\frac{1}{15}\right)...\left(1+\frac{1}{n^2+2n}\right)\)
\(=\frac{\left(1+1\right)^2}{1.\left(1+2\right)}.\frac{\left(2+1\right)^2}{2.\left(2+2\right)}.\frac{\left(3+1\right)^2}{3.\left(3+2\right)}...\frac{\left(n+1\right)^2}{n.\left(n+2\right)}\)
\(=\frac{\left[2.3.4...\left(n+1\right)\right]^2}{1.2.3...n.3.4.5...\left(n+2\right)}=\frac{\left[\left(n+1\right)!\right]^2}{n!.\frac{\left(n+2\right)!}{2}}\)
10 tháng 11 2021
a.\(A=\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}=\dfrac{\left(x-2\right)^2}{\left(x^2-4\right)\left(x-2\right)}=\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x+2}\)
10 tháng 11 2021
\(A=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}\left(x\ne\pm2\right)\\ A=\dfrac{\left(x-2\right)^2}{\left(x-2\right)^2\left(x+2\right)}=\dfrac{1}{x+2}\\ B=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\dfrac{4\sqrt{x}}{3}\left(x>0\right)\\ B=\dfrac{4\sqrt{x}\left(\sqrt{x}+1\right)}{3\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}\)
9 tháng 11 2021
\(a,=\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}=\sqrt{2}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}=-\sqrt{5}\\ c,=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{2}\)
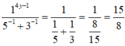
giúp tui nhé
\(A=\left(1+\frac{1}{3}\right)\left(1+\frac{1}{8}\right)...\left(1+\frac{1}{2499}\right)\)
\(A=\frac{2^2}{1.3}\frac{3^2}{2.4}...\frac{50^2}{49.50}\)
\(A=\frac{2^2.3^2...50^2}{1.3.2.4....49.51}\)
\(A=\frac{\left(2.3...50\right)\left(2.3...50\right)}{\left(1.2...49\right)\left(3.4...51\right)}\)
\(A=\frac{50.2}{51}=\frac{100}{51}\)