help mình vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT Bunhiacopxki (cho tất cả các bài):
1.
\(\left(3x+4y\right)^2\le\left(3^2+4^2\right)\left(x^2+y^2\right)=25\)
\(\Rightarrow\left|3x+4y\right|\le5\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{3}{5};\dfrac{4}{5}\right)\)
2.
\(\left(x+2y\right)^2=\left(1.x+\sqrt{2}.\sqrt{2y}\right)^2\le\left(1+2\right)\left(x^2+2y^2\right)=3\)
\(\Rightarrow\left|x+2y\right|\le\sqrt{3}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{1}{\sqrt{3}};\dfrac{1}{\sqrt{3}}\right)\)
4.
a.
Áp dụng Bunhiacopxki:
\(\left(b+c+c+a+a+b\right)\left(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow2\left(a+b+c\right)\left(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{a+b+c}{2}\)
Dấu "=" xảy ra khi \(a=b=c\)

\(ZnO,BaO,K_2O\)
\(ZnCl_2,BaCl_2,KCl\)
\(Zn\left(OH\right)_2,Ba\left(OH\right)_2,KOH\)
\(ZnSO_4,BaSO_4,K_2SO_4\)
\(Zn\left(NO_3\right)_2,Ba\left(NO_3\right)_2,KNO_3\)
\(ZnCO_3,BaCO_3,K_2CO_3\)
\(Zn_3\left(PO_4\right)_2,Ba_3\left(PO_4\right)_2,K_3PO_4\)




Câu 6)
\(U_{13}=U_{12}+U_{23}=2,4+2,5=4,9V\\ U_{23}=U_{13}-U_{12}=5,4V\\ U_{12}=U_{13}-U_{23}=11,7V\)
Câu 7)
\(I_1=I_2=0,25A\\ I_3=I-I_1\left(I_2\right)=0,1A\\ U=U_1=U_3=9V\\ U_2=U-U_1=3V\)

1/x + 1/y = 1/2
<=> 2/x + 2/y =1
<=> 2x + 2y = xy
<=> xy - 2x - 2y+4 =4
<=> (x-2).(y-2) =4
ta có các cặp (2;2),(-2;-2),(1;4), (-1;-4)
sau đó thử từng cặp một bạn nhé
cảm ơn bạn Thắng Hoàng nhưng có cái này mình ko hiểu lắm mấu chứa ẩn thì làm sao mà khử dc


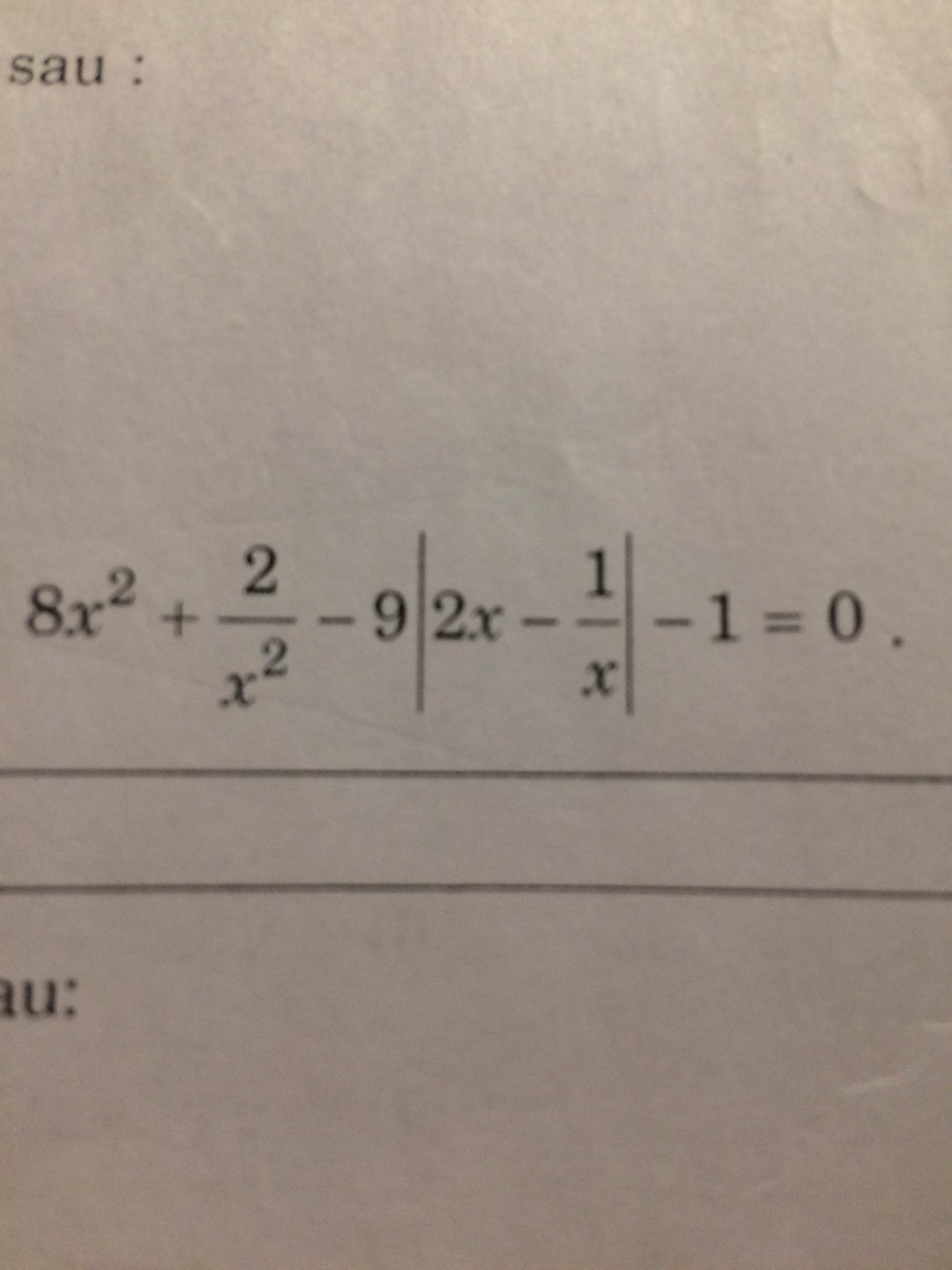
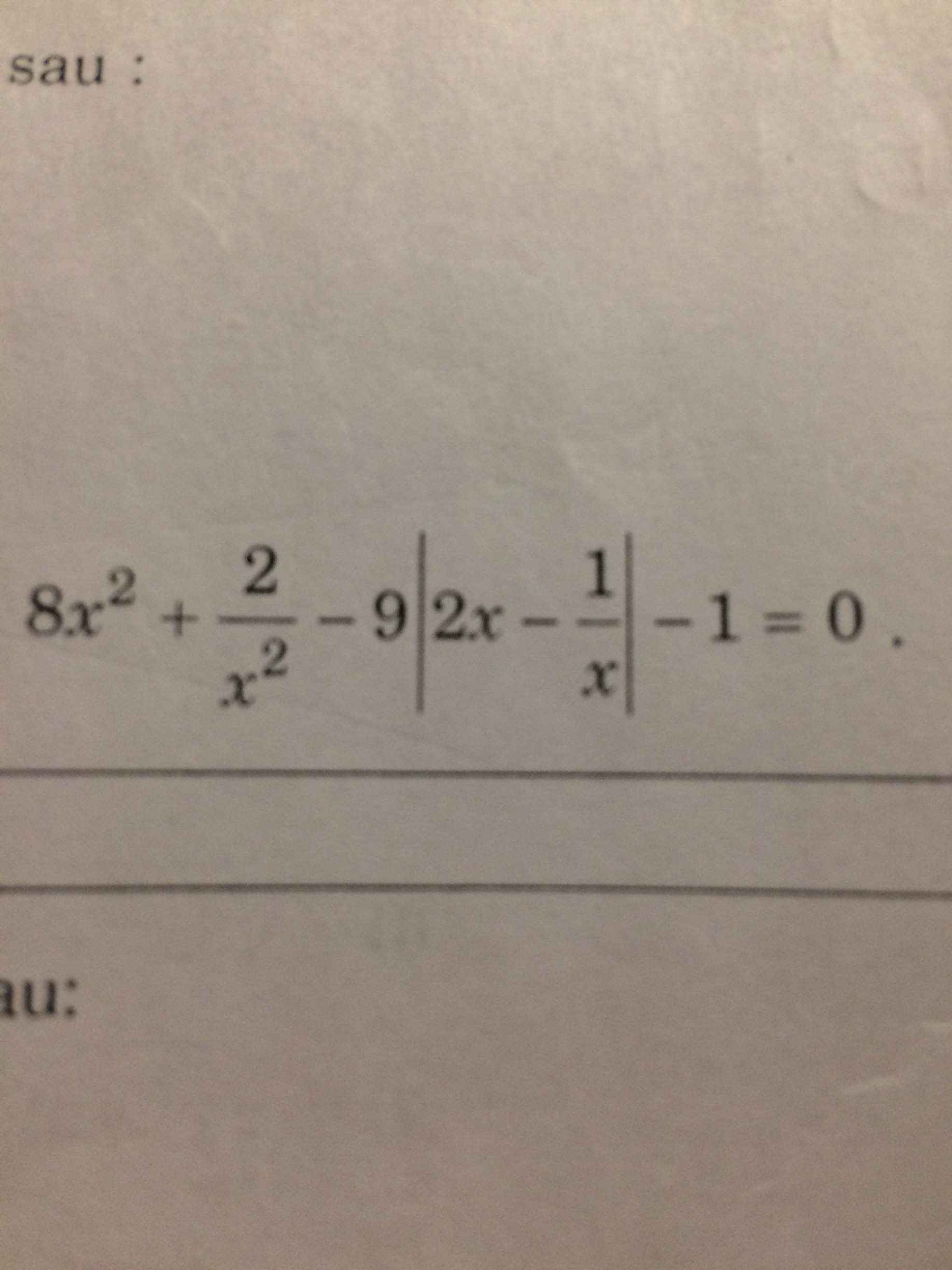
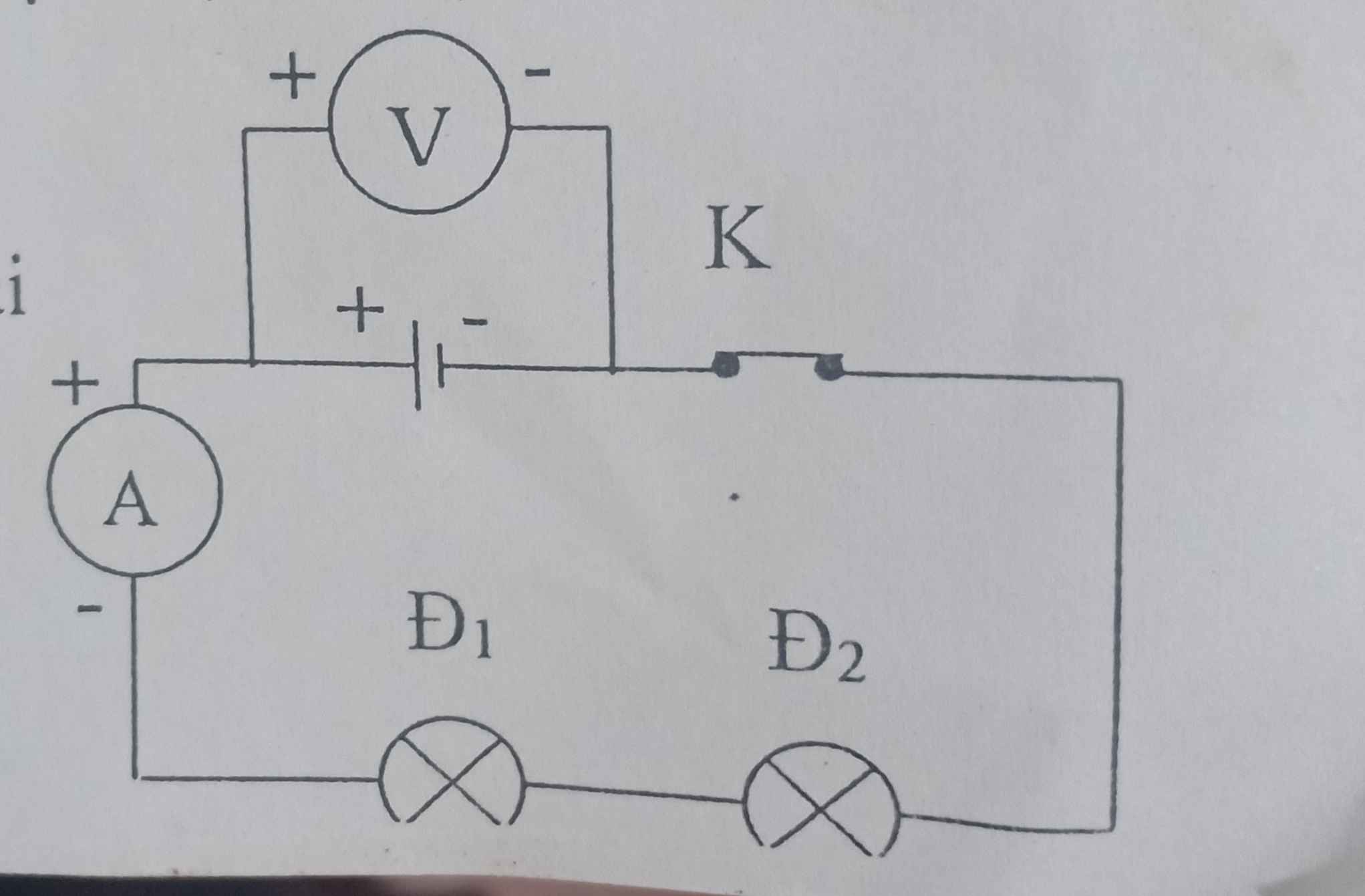
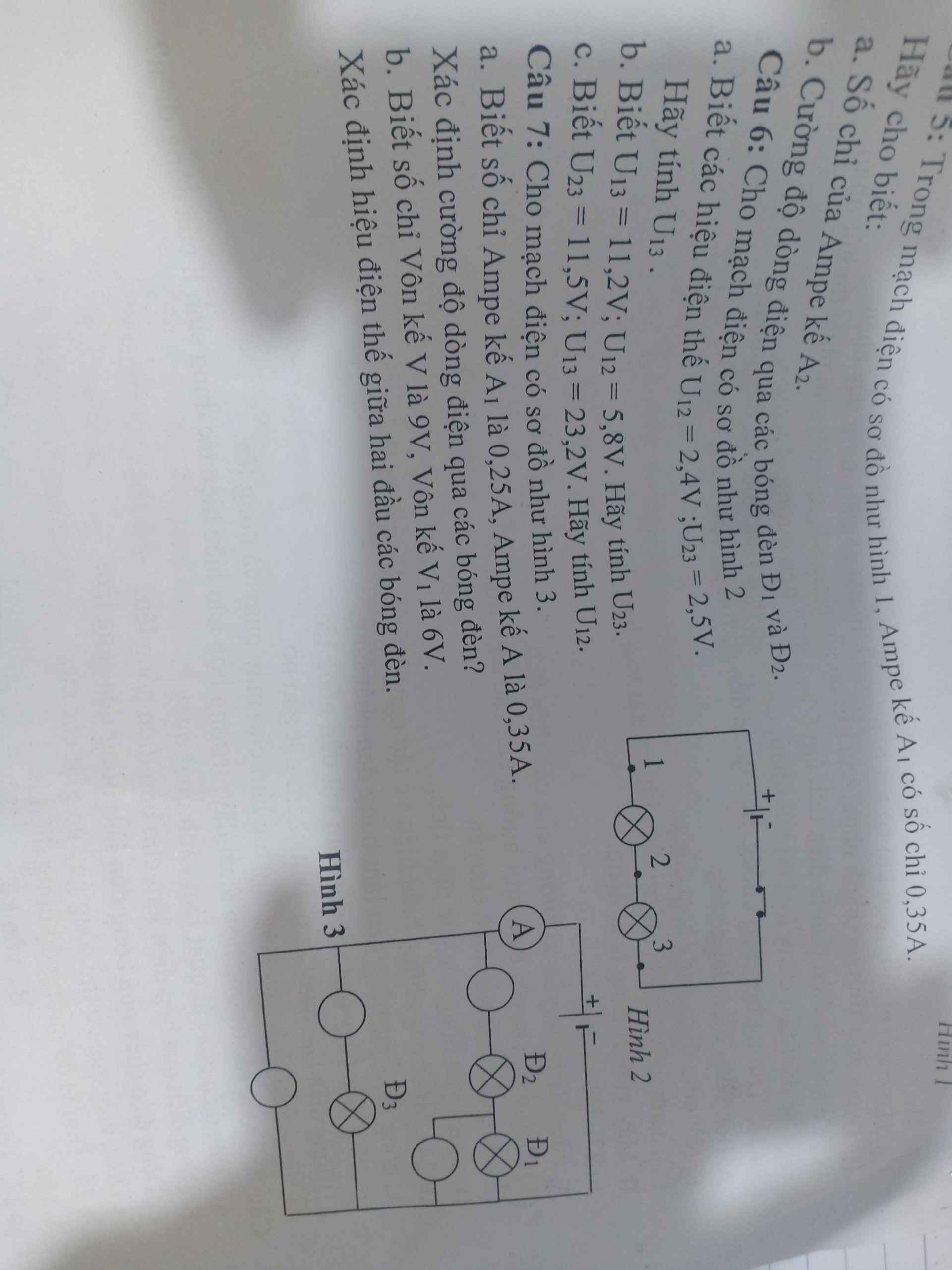 ai help mk vs mình đang cần gấp mai mk thi gòi plsssssssss
ai help mk vs mình đang cần gấp mai mk thi gòi plsssssssss