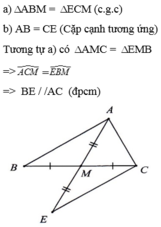
cho ΔABD,M là trung điểm của BC. trên tia đối của MA lấy điểm E sao cho ME=MA. Chúng minh:
a) ΔABM=ΔECM.
b) AB=CE và AC//BE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét \(\Delta\)ABM và \(\Delta\)ECM có:
BM = CM (M là trung điểm BC)
MA = ME (gt)
\(\widehat{AMB}=\widehat{EMC}\) (đối đỉnh)
\(\Rightarrow\) \(\Delta\)ABM = \(\Delta\)ECM (c-g-c)
b) Do \(\Delta ABM=\Delta ECM\left(cmt\right)\)
\(\Rightarrow AB=CE\) (hai cạnh tương ứng)
c) Xét \(\Delta ACM\) và \(\Delta EBM\) có:
CM = BM (M là trung điểm BC)
MA = ME (gt)
\(\widehat{AMC}=\widehat{BME}\) (đối đỉnh)
\(\Rightarrow\Delta ACM=\Delta EBM\left(c-g-c\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{E_1}\)
Mà \(\widehat{A_1}\) và \(\widehat{E_1}\) là hai góc so le trong
\(\Rightarrow\) AC // BE

Bạn tự vẽ hình nhé!
a/ Vì AB // CE nên \(\widehat{ABC}=\widehat{BCE}\)( vì là 2 góc so le trong )
Ta có: \(\widehat{AMB}=\widehat{CME}\)( vì là 2 góc đối đỉnh )
Xét tam giác AMB và tam giác CEM có:
\(\hept{\begin{cases}\widehat{ABC}=\widehat{BCE}\left(cmt\right)\\BM=MC\left(gt\right)\\\widehat{AMB}=\widehat{CME}\left(cmt\right)\end{cases}}\)
suy ra tam giác ABM = tam giác ECM ( g.c.g)
Nhớ k cho mình nhé! Thank you!!!

a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

Hình tự vẽ nha !
a/ Xét ΔABM và ΔECM có:
MB=MC (Mlà trung điểm của BC)
góc AMB = góc EMC ( 2 góc đối đỉnh)
MA=ME(giả thiết)
Do đó ΔABM=ΔECM(c.g.c)
b/ vì ΔABM=ΔECM nên góc BAM= góc MEC (2 góc tương ứng)
mà góc BAM và góc MEC là 2 góc ở vị trí so le trong ( khi đoạn thẳng AE cắt AB và CE ở A và E) nên theo dấu hiệu nhận biết 2 đường thẳng song song => AB // CE
c/ mik ko bt

Sửa đề: ΔABC vuông tại A
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
vậy: BC=10cm
b) Xét ΔAMC và ΔEMB có
CM=BM(M là trung điểm của BC)
\(\widehat{AMC}=\widehat{BME}\)(hai góc đối đỉnh)
MA=ME(gt)
Do đó: ΔAMC=ΔEMB(c-g-c)
Suy ra: AC=BE(hai cạnh tương ứng)
Xét ΔAMB và ΔEMC có
AM=EM(gt)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔEMC(c-g-c)
Suy ra: \(\widehat{BAM}=\widehat{CEM}\)(hai góc tương ứng)
mà \(\widehat{BAM}\) và \(\widehat{CEM}\) là hai góc ở vị trí so le trong
nên AB//EC(Dấu hiệu nhận biết hai đường thẳng song song)