gọi x0 là nghiệm của phương trình 3x - 10 = 0. tính giá trị của biểu thức Q = 3x0 -2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 1 2017
Chọn C.
Điều kiện. x ≠ -1
Phương trình tương đương 
Lấy ln hai vế của , ta được 
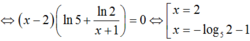
Suy ra x0 = 2 và P = 60.
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 7 2021
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=1\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=3^2-2.1=7\)
16 tháng 11 2021
\(F=x_1^2-3x_2-2013\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-7\end{matrix}\right.\)
Vì \(x_1\) là nghiệm của PT nên \(x_1^2+3x_1-7=0\Leftrightarrow x_1^2=7-3x_1\)
\(\Leftrightarrow F=7-3x_1-3x_2-2013\\ F=-2006-3\left(x_1+x_2\right)=-2006-3\left(-3\right)=-1997\)
17 tháng 1 2021
a) Ta có: \(2x^2-3x-2=0\)
nên a=2; b=-3 và c=-2
Vì \(x_1\) và \(x_2\) là nghiệm của phương trình \(2x^2-3x-2=0\) nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{3}{2}\\x_1\cdot x_2=-\dfrac{2}{2}=-1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=-1\)
nên \(2\cdot x_1\cdot x_2=-2\)
Ta có: \(\left(x_1+x_2\right)^2=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\)
\(\Leftrightarrow x_1^2+x_2^2+2\cdot x_1\cdot x_2=\dfrac{9}{4}\)
\(\Leftrightarrow x_1^2+x_2^2=\dfrac{9}{4}+2=\dfrac{17}{4}\)
.
20 tháng 6 2023
a: a*c<0
=>(1) có hai nghiệm phân biệt
b: Bạn viết lại biểu thức đi bạn
2
13 tháng 1 2023
`1)` Ptr có: `\Delta=3^2-4.5.(-1)=29 > 0 =>`Ptr có `2` nghiệm phân biệt
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=-3/5),(x_1.x_2=c/a=-1/5):}`
Có: `A=(3x_1+2x_2)(3x_2+x_1)`
`A=9x_1x_2+3x_1 ^2+6x_2 ^2+2x_1x_2`
`A=8x_1x_2+3(x_1+x_2)^2=8.(-1/5)+3.(-3/5)^2=-13/25`
Vậy `A=-13/25`
____________________________________________________
`2)` Ptr có: `\Delta'=(-1)^2-7.(-3)=22 > 0=>` Ptr có `2` nghiệm pb
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=2/7),(x_1.x_2=c/a=-3/7):}`
Có: `M=[7x_1 ^2-2x_1]/3+3/[7x_2 ^2-2x_2]`
`M=[(7x_1 ^2-2x_1)(7x_2 ^2-2x_2)+9]/[3(7x_2 ^2-2x_2)]`
`M=[49(x_1x_2)^2-14x_1 ^2 x_2-14x_1 x_2 ^2+4x_1x_2+9]/[3(7x_2 ^2-2x_2)]`
`M=[49.(-3/7)^2-14.(-3/7)(2/7)+4.(-3/7)+9]/[3x_2(7x_2-2)]`
`M=6/[x_2(7x_2-2)]` `(1)`
Có: `x_1+x_2=2/7=>x_1=2/7-x_2`
Thay vào `x_1.x_2=-3/7 =>(2/7-x_2)x_2=-3/7`
`<=>-x_2 ^2+2/7 x_2+3/7=0<=>x_2=[1+-\sqrt{22}]/7`
`@x_2=[1+\sqrt{22}]/7=>M=6/[[1+\sqrt{22}]/7(7 .[1+\sqrt{22}]/2-2)]=2`
`@x_2=[1-\sqrt{22}]/7=>M=6/[[1-\sqrt{22}]/7(7 .[1-\sqrt{22}]/2-2)]=2`
Vậy `M=2`
\(x_0=\dfrac{10}{3}\)
\(\Leftrightarrow Q=3\cdot\dfrac{10}{3}-2=10-2=8\)