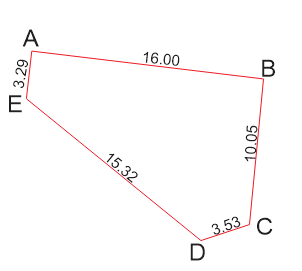
 Hi cả nhà Mình lâu quá không sử dụng công thức tính diện tích nên quên nhờ cả nhà giải hộ ạ
Hi cả nhà Mình lâu quá không sử dụng công thức tính diện tích nên quên nhờ cả nhà giải hộ ạ
Công thức tính diện tích hình thoi S Area, cách tính diện tích hình thoi lớp 4 cạnh a
1. Hình Thoi là gì?
Hình thoi là hình tứ giá có 4 cạnh bằng nhau và có một số tính chất như: 2 góc đối bằng nhau, 2 đường chéo vuông góc với nhau và cắt tại trung điểm của mỗi đường đồng thời là đường phân giác của các góc. Hình thoi có đầy đủ các tính chất của hình bình hành
2. Công thức tính diện tích hình thoi
Diện tích hình thoi bằng 1 nửa tích của 2 đường chéo
Hình thoi ABCD với 2 đường chéo d1 d2
Công thức tính diện tích hình thoi
với d1 d2 lần lượt là 2 đường chéo của hình thoi
Công thức tính chu vi của hình thoi
Với a là chiều dài của cạnh hình thoi
Một số bạn thắc mắc rằng tại sao diện tích hình thoi lại yêu cầu tính chiều cao của hình thoi rồi từ đó tính diện tích. Vì Hình thoi có đầy đủ tính chất của hình bình hành nên các bạn có thể áp dụng tính diện tích hình bình hành hoặc kể cả hình thang để tính diện tích hình thoi.




