1.So sánh các góc của ∆ABC biết rằng: AB 4cm BC 5cm CA 5cm. 2.So sánh các góc của ∆ABC biết rằng: AB BC CA , lần lượt tỉ lệ với2;3;4.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
5 tháng 8 2019
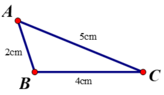
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
YT
2
11 tháng 3 2023
Theo định lý `1` của tam giác `->`\(\widehat{B}>\widehat{A}>\widehat{C}\)
PT
1
CM
31 tháng 1 2017
Ta có: AB = BC nên ΔABC cân tại B
Suy ra: ∠A = ∠C
Vì BC > AC nên ∠A > ∠B (đối diện cạnh lớn hơn là góc lớn hơn)
Vậy ∠A = ∠C > ∠B .
HV
0
TU
4
10 tháng 7 2018
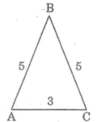
Ta có : AB = 5cm ; BC = 5cm ; AC = 3cm
\(\Rightarrow\)AB = BC = 5cm
AB > AC ( 5cm > 3cm )
AC < BC ( 3cm < 5cm )
Chúc bn hok tốt
10 tháng 7 2018
Ta có: AB = BC nên ΔABC cân tại B
Suy ra: \(\widehat{A}=\widehat{C}\)
Vì BC > AC nên \(\widehat{A}>\widehat{B}\) (đối diện cạnh lớn hơn là góc lớn hơn)
Vậy \(\widehat{A}=\widehat{C}>\widehat{B}\)
SG
3
19 tháng 4 2017
Trong tam giác ABC có:
AB = 2cm ; BC = 4cm ; AC = 5cm
=> AB < BC < CA nên
B
3
18 tháng 1
a: Xét ΔABC có AB<AC<BC
mà \(\widehat{C};\widehat{B};\widehat{A}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Vì \(\widehat{C}< \widehat{B}< \widehat{A}\)
nên \(\widehat{A}\) là góc lớn nhất trong ΔABC
SG
2
19 tháng 6 2017
từ đề bài, ta có:
AB = BC >AC
\(\Rightarrow\widehat{C}=\widehat{A}>\widehat{B}\)
22 tháng 2 2021
Xét ΔABC có AB=BC>AC(5cm=5cm>3cm)
mà góc đối diện với cạnh AB là \(\widehat{C}\)
góc đối diện với cạnh BC là \(\widehat{A}\)
góc đối diện với cạnh AC là \(\widehat{B}\)
nên \(\widehat{C}=\widehat{A}>\widehat{B}\)
giúp mik với
1.
AB<BC=CA
=>A<B=C
2