tam giác ABC đều gọi DEF lần lượt là trung điểm AB,AC và BC.Trên tia đối của tia AB lấy điểm M sao cho AM=DA.Trên tia đối của CA lấy điểm N sao cho CE=CN.Trên tia đối của BC lấy điểm P sao cho BP=BF a: chứng minh tam giác MNP đều b: chứng minh MED vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a Xét tứ giác ABCM có
D là trung điểm chun của AC và BM
=>ABCM là hình bình hành
=>AM//BC và AM=BC
b: Xét tứ giác ANBC có
E là trung điểm chung của AN và BC
=>ANBC là hình bình hành
=>AN//BC và AN=BC
=>M,A,N thẳng hàng

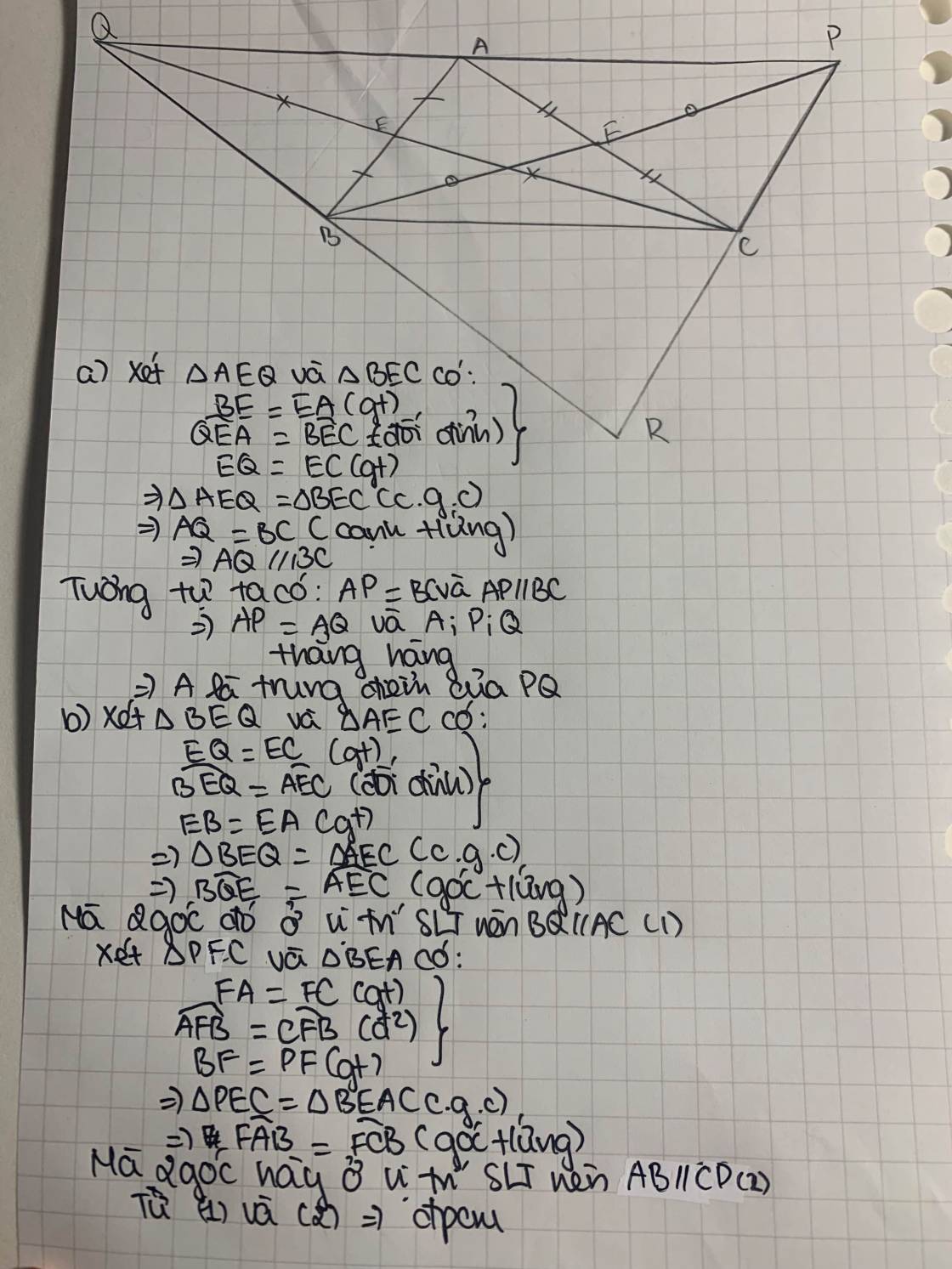
a) Xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=> tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ.

#\(N\)
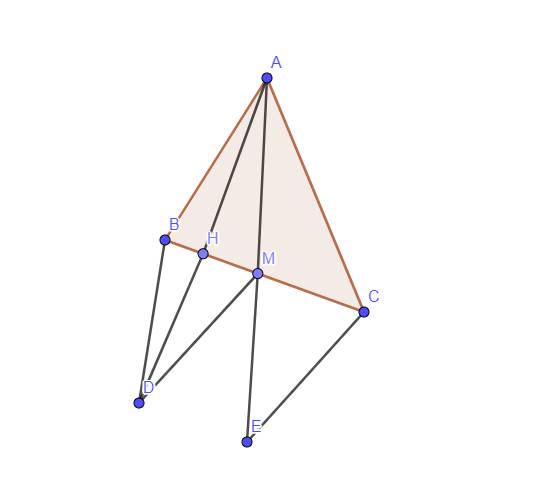
`a,` Xét Tam giác `AMB` và Tam giác `CME` có:
`AM = ME (g``t)`
\(\widehat{AMB}=\widehat{CME}\) `(2` góc đối đỉnh `)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `CME (c-g-c)`
`b,` Vì Tam giác `AMB =` Tam giác `CME (a)`
`-> AB = CE (2` cạnh tương ứng `)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{BHA}=\widehat{BHD}=90^0\)
`BH` chung
`=>` Tam giác `ABH =` Tam giác `DBH (c-g-c)`
`=> AB = BD (2` cạnh tương ứng `)`
Mà `AB = CE -> BD = CE`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`HA = HD (g``t)`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HM` chung
`=>` Tam giác `AMH =` Tam giác `DMH (c-g-c)`
`=> AM = DM (2` cạnh tương ứng `)`
Xét Tam giác `AMD` có: `AM = DM`
`->` Tam giác `AMD` là tam giác cân.


a) Ta có: ΔABC đều(gt)
⇒AB=AC=BC
mà AD=DB=AB/2 (Dlà trung điểm của AB)
và AE=EC=AC/2 (Elà trung điểm của AC)
và BF=FC=BC/2(F là trung điểm của BC)
nên AD=DB=AE=EC=BF=FC(1)
Xét ΔABC có
D là trung điểm của AB(gt)
E là trung điểm của AC(gt)
Do đó: DE là đường trung bình của ΔABC(định nghĩa đường trung bình của tam giác)
⇒DE//BC và DE=BC/2(định lí 2 về đường trung bình của tam giác)
mà BF=FC=BC/2(F là trung điểm của BC)
nên DE=BF=FC(2)
Xét tứ giác BDEF có DE//BF(DE//BC, F∈BC) và DE=BF(cmt)
nên BDEF là hình bình hành(dấu hiệu nhận biết hình bình hành)
Hình bình hành BDEF có BD=BF(cmt)
nên BDEF là hình thoi(dấu hiệu nhận biết hình thoi)
b) Ta có: DE=EM(gt)
mà D,E,M thẳng hàng
nên E là trung điểm của DM
Xét tứ giác AMCD có
E là trung điểm của đường chéo AC(gt)
E là trung điểm của đường chéo DM(cmt)
Do đó: AMCD là hình bình hành(dấu hiệu nhận biết hình bình hành)
Từ (1) và (2) suy ra AD=DB=BF=FC=CE=AE=DE
hay DE=AE
mà DM=2*DE(E là trung điểm của DM)
và AC=2*AE(E là trung điểm của AC)
nên DM=AC
Xét hình bình hành AMCE có DM=AC(cmt)
nên AMCE là hình chữ nhật(dấu hiệu nhận biết hình chữ nhật)