trong mặt phẳng với hệ trục tọa độ Oxy, cho hình vuông ABCD có tâm là điểm I. Gọi G(-1/3;0) và K(-1/3;-5/3) lần lượt là trọng tâm các tam giác ABI và ACD. Biết A(a;b) với a là số nguyên. Khi đó a^2+b^2 bằng bao nhiêu? giup em voi em cam on nhieu lammmm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Hình chiếu vuông góc của M(2;-1;4) lên mặt phẳng (Oxy) là điểm H(2;-1;0).

I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)

Phương trình đường thẳng AM: \(ax+by-\dfrac{11}{2}a-\dfrac{1}{2}b=0\left(a^2+b^2\ne0\right)\)
Giả sử cạnh hình vuông có độ dài là \(a\)
\(AM^2=\dfrac{5}{4}a^2;AN^2=\dfrac{10}{9}a^2;MN^2=\dfrac{25}{36}a^2\)
Theo định lí cos: \(cosMAN=\dfrac{AM^2+AN^2-MN^2}{2.AM.AN}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\dfrac{\left|2a-b\right|}{\sqrt{5\left(a^2+b^2\right)}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left(a-3b\right)\left(3a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=3b\\3a=-b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AM:3x+y-17=0\\AM:x-3y-4=0\end{matrix}\right.\)
TH1: \(AM:3x+y-17=0\Rightarrow A:\left\{{}\begin{matrix}3x+y-17=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(4;5\right)\)
TH2: \(AM:x-3y-4=0\Rightarrow A:\left\{{}\begin{matrix}x-3y-4=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(1;-1\right)\)
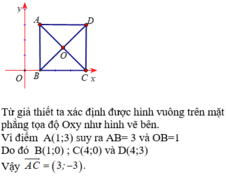
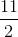

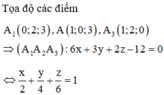


Đặt tên điểm như hình vẽ bên dưới
Ta có: F là trung điểm BI \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AF}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)=\dfrac{1}{3}\left(\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\)
\(\overrightarrow{AH}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AK}=\dfrac{2}{3}\overrightarrow{AH}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\)
\(\overrightarrow{GK}=\overrightarrow{GA}+\overrightarrow{AK}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{6}\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AG}.\overrightarrow{GK}=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)=-\dfrac{1}{12}AB^2+\dfrac{1}{12}AD^2=0\)
\(\Rightarrow AG\perp GK\)
\(\left\{{}\begin{matrix}\overrightarrow{GA}=\left(a+\dfrac{1}{3};b\right)\\\overrightarrow{KG}=\left(0;\dfrac{5}{3}\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{GA}.\overrightarrow{KG}=\left(a+\dfrac{1}{3}\right).0+\dfrac{5}{3}b=0\Rightarrow b=0\)
Mặt khác: \(AG^2-GK^2=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)^2-\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)^2=0\)
\(\Rightarrow AG^2=GK^2\Rightarrow\left(a+\dfrac{1}{3}\right)^2=\left(\dfrac{5}{3}\right)^2\Rightarrow a=-2\)