Cho tam giác ABC cân tại ,kẻ BD vuông góc AC,CE vuông góc AB
Cm.a)BD=CE
b)AD=AE
c)Gọi I là giao điểm BD và CE .Cm IE=ID
d)AI là p.giác
e)AI vuông góc BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 1 2022
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔAED có AE=AD
nên ΔAED cân tại A
c: Xét ΔEBI vuông tại E và ΔDCI vuông tại D có
EB=DC
\(\widehat{EBI}=\widehat{DCI}\)
Do đó; ΔEBI=ΔDCI
Suy ra: IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
3 tháng 3 2022
a: Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔBEC=ΔCDB
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó:ΔABD=ΔACE
Suy ra: AD=AE
c: Ta có: ΔBEC=ΔCDB
nên \(\widehat{IBC}=\widehat{ICB}\)
hayΔIBC cân tại I
Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó:ΔABI=ΔACI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
d: Xét ΔABC có AE/AB=AD/AC
nên DE//BC
N
18 tháng 1 2021
Sửa lại đề : A < 90*
a, Chứng minh
\(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
\(\RightarrowĐPCM\)
b, CM được :
\(\widehat{ADE}\)\(=\)\(\widehat{ACB}\)\(=\)\(\frac{180'-\widehat{BAC}}{2}\)
\(\Rightarrow DE//BC\)
c, CM được : \(\widehat{IBC}=\widehat{ICB}\)
\(\RightarrowĐPCM\)
d, Gọi M là giao điểm của AI và BC ,
CM được AI là tia phân giác của góc \(\widehat{BAC}\), từ đó \(\widehat{AMB}\)\(=90'\)
\(\RightarrowĐPCM\)
13 tháng 3 2020
bạn ơi bạn có nhầm đề không sao góc A < 900??? Bạn xem lại đề nhé
11 tháng 1 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc A chung
Do đó; ΔADB=ΔAEC
=>AD=AE
b: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
c: Xét ΔIBC có góc IBC=góc ICB
nên ΔiBC cân tại I
=>IB=IC
d: AB=AC
IB=IC
=>AI là trung trực của BC
=>AI vuông góc với BC
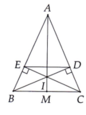
a) Xét tam giác AEC và tam giác ADB:
+ AC = AB (Tam giác ABC cân tại A).
+ \(\widehat{A}chung.\)
+ \(\widehat{AEC}=\widehat{ADB}=90^o.\)
\(\Rightarrow\) Tam giác AEC = Tam giác ADB (cạnh huyền - góc nhọn).
\(\Rightarrow\) BD = CE (2 cạnh tương ứng).
b) Tam giác AEC = Tam giác ADB (cmt).
\(\Rightarrow\) AD = AE (2 cạnh tương ứng).
c) Xét tam giác AEI và tam giác ADI:
+ AI chung.
+ AE = AD (cmt).
+ \(\widehat{AEI}=\widehat{ADI}=90^o.\)
\(\Rightarrow\) Tam giác AEI = Tam giác ADI (canh huyền - cạnh góc vuông).
\(\Rightarrow\) IE = ID (2 cạnh tương ứng).
d) Tam giác AEI = Tam giác ADI (cmt).
\(\Rightarrow\) \(\widehat{EAI}=\widehat{DAI}\) (2 góc tương ứng).
\(\Rightarrow\) AI là phân giác \(\widehat{A}.\)
e) Xét tam giác ABC cân tại A:
AI là phân giác \(\widehat{A}\left(cmt\right).\)
\(\Rightarrow\) AI là đường cao (Tính chất tam giác cân).
\(\Rightarrow\) \(AI\perp BC.\)