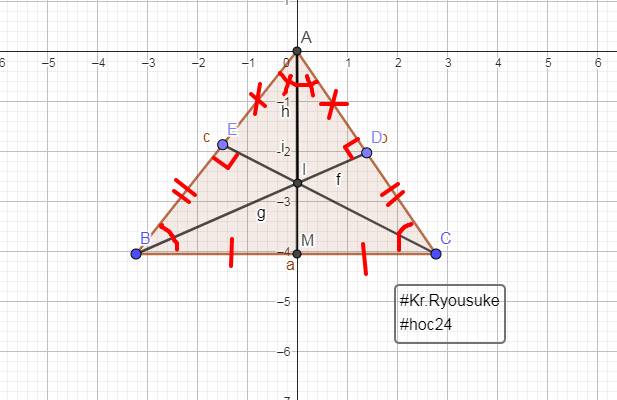
Cho tam giác ABC (AB < AC). Kẻ AM là tia phân giác của góc A (M thuộc BC). TrênAC lấy điểm D sao cho AB = AD.a) Chứng minh: AABM = AADMb) Gọi I là giao điểm của AM và BD. Chứng minh: AI 1 BD.c) Kéo dà...

PP

Phạm Phương Tùng

7 tháng 1 2022 - olm

Cho tam giác ABC (AB < AC). Kẻ AM là tia phân giác của góc A (M thuộc BC). TrênAC lấy điểm D sao cho AB = AD.a) Chứng minh: AABM = AADMb) Gọi I là giao điểm của AM và BD. Chứng minh: AI 1 BD.c) Kéo dài DM cắt AB tại H. Chứng minh: AMBH = AMDCd) Gọi P là trung điểm của đoạn HC. Chứng minh: ba điểm A, M, P thẳng...

Đọc tiếp

#Toán lớp 7

0

YT

Yoriichi Tsugikuni

6 tháng 12 2023

Cho △ABC có AB < AC. Kẻ AM là tia phân giác của góc A (M ∈ BC). Trên AC lấy điểm D sao cho AB = AD.a) Chứng minh rằng △ABM = △ADM.b) Gọi I là giao điểm của AM và BD. Chứng minh rằng AI ⊥ BD.c) Kéo dài DM cắt AB tại H. Chứng minh rằng △MBH = △MDC.d) Gọi P là trung điểm của đoạn HC. Chứng minh rằng 3 điểm A; M; P thẳng...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

6 tháng 12 2023

a: Xét ΔABM và ΔADM có

AB=AD

$\widehat{BAM}=\widehat{DAM}$

AM chung

Do đó: ΔABM=ΔADM

b: Xét ΔABD có AB=AD

nên ΔABD cân tại A

Ta có: ΔABD cân tại A

mà AI là đường phân giác

nên AI$\perp$BD tại I

c: ΔABM=ΔADM

=>$\widehat{ABM}=\widehat{ADM}$

Ta có: $\widehat{ABM}+\widehat{HBM}=180^0$(hai góc kề bù)

$\widehat{ADM}+\widehat{CDM}=180^0$(hai góc kề bù)

mà $\widehat{ABM}=\widehat{ADM}$

nên $\widehat{HBM}=\widehat{CDM}$

ΔABM=ΔADM

=>MB=MD

Xét ΔMBH và ΔMDC có

$\widehat{MBH}=\widehat{MDC}$

MB=MD

$\widehat{BMH}=\widehat{DMC}$

Do đó: ΔMBH=ΔMDC

d: ΔMBH=ΔMC

=>BH=DC và MH=MC

AB+BH=AH

AD+DC=AC
mà AB=AD và BH=DC

nên AH=AC

=>A nằm trên đường trung trực của HC(1)

MH=MC

=>M nằm trên đường trung trực của HC(2)

PH=PC

=>P nằm trên đường trung trực của HC(3)

Từ (1),(2),(3) suy ra A,P,M thẳng hàng

Đúng(2)

JP

Jack!! Pro

21 tháng 12 2022

Cho tam giác ABC (AB < AC). KẻAM là tia phân giác của góc A (M thuộc BC). Trên AC lấy điểm D sao cho AB = AD. a) Chứng minh: ∆ABM = ∆ADM b) Gọi I là giao điểm của AM và BD. Chứng minh: AI ⊥ BD. c) Kéo dài DM cắt AB tại H. Chứng minh: ∆MBH = ∆MDC d) Gọi P là trung điểm của đoạn HC. Chứng minh: ba điểm A, M, P thẳng...

Đọc tiếp

#Toán lớp 7

3

JP

Jack!! Pro

21 tháng 12 2022

Mọi người giúp mik vs ạ

Đúng(0)

M

minh :)))

21 tháng 12 2022

sáng vừa làm xong_{bài này dài lắm với lại lm lâu nx}

Đúng(0)

QM

Quên Mất Tên Rồi

9 tháng 12 2016

Cho tam giác ABC có AB bé hơn AC, AM là tia phân giác của góc A ( M thuộc BC ). Trên tia AC lấy điểm D sao cho AD=AB

a) Chứng minh BM=MD

b) Gọi K là giao điểm của AB và DM. Chứng minh tam giác tam giác DAK=tam giác BAC

c) Chứng minh AM là đường trung trực của đoạn thẳng BD

#Toán lớp 7

1

CN

Chuẩn Nguyễn

23 tháng 6 2017

gải giúp em vs ạ

Đúng(0)

BF

Blox Fruits VN

6 tháng 12 2021

Bài 1: Cho tam giác ABC(AB<AC), AD là tia phân giác của góc BAC(D∈BC). Trên cạnh AC lấy điểm M sao cho AM=AB

1) Chứng minh △ABD=△AMD

2) Gọi I là giao điểm của AD và BM. Chứng minh I là trung điểm của BM và AI ⊥BM.

3) Gọi K là trung điểm của AM, trên tia đối của tia KB lấy điểm P sao cho KB=KP. Chứng minh MP//AB

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

6 tháng 12 2021

1: Xét ΔABD và ΔAMD có

AB=AM

$\widehat{BAD}=\widehat{MAD}$

AD chung

Do đó: ΔABD=ΔAMD

Đúng(0)

BF

Blox Fruits VN

6 tháng 12 2021

Bài 1: Cho tam giác ABC(AB<AC), AD là tia phân giác của góc BAC(D∈BC). Trên cạnh AC lấy điểm M sao cho AM=AB

1) Chứng minh △ABD=△AMD

2) Gọi I là giao điểm của AD và BM. Chứng minh I là trung điểm của BM và AI ⊥BM.

3) Gọi K là trung điểm của AM, trên tia đối của tia KB lấy điểm P sao cho KB=KP. Chứng minh MP//AB

#Toán lớp 7

2

BF

Blox Fruits VN

6 tháng 12 2021

giúp tui nha

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

6 tháng 12 2021

1: Xét ΔABD và ΔAMD có

AB=AM

$\widehat{BAD}=\widehat{MAD}$

AD chung

Do đó: ΔABD=ΔAMD

Đúng(0)

HK

Huỳnh Kim Uyên

28 tháng 3 2022

Cho tam giác ABC cân tại A, AM là phân giác góc A (M thuộc BC)

a/ chứng minh MB = MC

b/ Gọi I là trung điểm AC. Trên tia đối của tia đối của tia IB, lấy D sao cho BI = ID. Chứng minh AB // CD

c/ Gọi K là giao điểm của AM và CD. Chứng minh KC + IB + CD > AM + IA

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 7 2023

a: Xét ΔABM và ΔACM có

AB=AC

góc BAM=góc CAM

AM chung

=>ΔABM=ΔACM

=>MB=MC

b: Xét tứ giác ABCD có

I là trung điểm chung của AC và BD

=>ABCD là hình bình hành

=>AB//CD

Đúng(0)

CL

cu llor con

15 tháng 5 2023

Cho tam giác ABC cân tại A(A<90độ),kẻ CE⊥AB(E thuộc AB),BD⊥AC(d thuộc AC).
a) chứng minh BE=CD
b) Gọi I là giao điểm của BD và CE.chứng minh AI là tia phân giác của góc BAC.
c) Gọi M là trung điểm của BC, chứng minh ba điểm A,I,M thảng hàng.

#Toán lớp 7

2

NL

Nguyễn Lê Phước Thịnh

15 tháng 5 2023

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có

BC chung

góc EBC=góc DCB

=>ΔEBC=ΔDCB

=>BE=DC

=>AE=AD

b: Xét ΔAEI vuông tại E và ΔADI vuông tại D có

AI chung

AE=AD

=>ΔAEI=ΔADI

=>góc EAI=góc DAI

=>AI là phân giác của góc BAC

c: ΔABC cân tại A

mà AM là trung tuyến

nên AM là phân giác của góc BAC

=>A,I,M thẳng hàng

Đúng(2)

KT

『Kuroba ム Tsuki Ryoo ︵²ᵏ⁷』

15 tháng 5 2023

`a,`

Vì `\Delta ABC` cân tại A

`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$

Xét `2\Delta` vuông và `BEC` và `CDB`:

`\text {BC chung}`

$\widehat {B} = \widehat {C}$

`=> \Delta BEC = \Delta CDB (ch-gn)`

`-> \text {BE = CD (2 cạnh tương ứng)}`

`b,`

Ta có: $\left\{{}\begin{matrix}\text{AB = AE + BE}\\\text{AC = AD + CD}\end{matrix}\right.$

Mà $\left\{{}\begin{matrix}\text{AB = AC}\\\text{BE = CD}\end{matrix}\right.$

`-> \text {AE = AD}`

Xét `2\Delta` vuông `AEI` và ` ADI`:

`\text {AE = AD}`

`\text {AI chung}`

`=> \Delta AEI = \Delta ADI (ch-cgv)`

`->` $\widehat {EAI} = \widehat {DAI} (\text {2 góc tương ứng})$

`-> \text {AI là tia phân giác của}` $\widehat {EAD}$

Mà $\text{E}\in\text{AB, D}\in\text{AC}$

`-> \text {AI là tia phân giác của}` $\widehat {BAC}$ `(1)`

`c,`

Vì M là trung điểm của AC

`-> \text {AM là đường trung tuyến của} \Delta ABC` `(2)`

Từ `(1)` và `(2)`

`-> \text {Ba điểm A, I, M thẳng hàng.}`

loading...

Đúng(2)

NT

Nguyễn Trần Minh Thư

20 tháng 4 2017 - olm

Cho tam giác ABC vuông tại A, trên tia đối của tia AB lấy điểm D sao cho AD = AB

a. Chứng minh tam giác CDB cân và CA phân giác góc BCD.

b. Kẻ Am song song với BC (M thuộc DC)

Chứng minh M là trung điểm DC.

c. Gọi O thuộc AC sao cho OA=1/3AC. Chứng minh B, M, O thẳng hàng

d. Gọi N là giao điểm của DO và BC.

Chứng minh NM song song với BD và MN = AD

#Toán lớp 7

0

TV

toàn văn

1 tháng 12 2021

cho tam giác abc có AB=AC,gọi AM là tia phân giác của góc A(M thuộc BC)

a Chứng minh tam giác AMB = tam giác AMC

b Chứng minh M là trung điểm của cạnh BC và AM ⊥ BC

c Trên tia AM lấy điểm K sao cho MA = MK. Chứng minh AB = CK và AB // CK

#Toán lớp 7

0

TA

Thu Anh

29 tháng 11 2021

: Cho tam giác ABC có AB = AC, gọi AM là tia phân giác của góc A(M thuộc BC). a) Chứng minh tam giác AMB = tam giác AMC

b) Chứng minh M là trung điểm của cạnh BC và AM ⊥ BC.

c) Trên tia AM lấy điểm K sao cho MA = MK. Chứng minh AB = CK và AB // CK

#Toán lớp 7

1

M

Mr_Johseph_PRO

29 tháng 11 2021

a

vì AM là tia phân giác của góc A=>góc BAM=CAM

xét tam giác AMB và tam giác AMC có:

góc BAM=CAM,AM chung,AB=AC=>tam giác AMB = tam giác AMC

b

vì tam giác AMB = tam giác AMC=>MB=MC=>M là trung điểm BC

vì tam giác AMB = tam giác AMC=>góc BAM=CAM mà góc BAM+CAM=180=>BAM=CAM=180 độ/2=90 độ=>AM vuông góc với BC

c

xét tam giác ABM và KCM có

MB=MC,MA=MK,góc BMA=CMK(vì đối đỉnh)=>tam giác ABM = KCM=>AB=CK

vì tam giác ABM = KCM=>góc ABM=KMB mà 2 góc trên ở vị trí so le trog=>AB//CK

Đúng(1)

S

Sunn

29 tháng 11 2021

Xài Telex cho nóa đẹp đy !

Đúng(2)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP