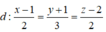KHoảng cách giữa 2 đường thẳng d: 2x - y +3 =0 và d' \(\left\{{}\begin{matrix}x=3+t\\y=4+2t\end{matrix}\right.\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



NX: \(\dfrac{2}{4}\)=\(\dfrac{-1}{-2}\)≠\(\dfrac{-2}{6}\)
=> (d) // (d')
Ta lấy điểm A(0;-2) ∈ d
d(d;d') = \(\dfrac{\left|4.0-2.\left(-2\right)+6\right|}{\sqrt{4^2+2^2}}\) = \(\sqrt{5}\)
=> Chọn C

\(1/\)
\(M\left(3;5\right);d:x+y+1=0\)
\(\)Gọi khoảng cách từ M đến d là \(l\)
\(l\left(M;d\right)=\dfrac{\left|x_M+y_M+1\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|3+5+1\right|}{\sqrt{1^2+1^2}}=\dfrac{9\sqrt{2}}{2}\)
\(M\left(2;3\right);d:\left\{{}\begin{matrix}x-2t\\y=2+3t\end{matrix}\right.\)
d qua \(M\left(2;3\right)\) có \(VTCP\overrightarrow{u}=\left(-2;3\right)\Rightarrow VTPT\overrightarrow{n}=\left(3;2\right)\)
\(PTTQ\) của \(\Delta:3\left(x-2\right)+2\left(y-3\right)=0\)
\(\Rightarrow3x-6+2y-6=0\)
\(\Rightarrow3x+2y-12=0\)
Gọi khoảng cách từ M đến d là \(l\)
\(l\left(M;d\right)=\dfrac{\left|3.x_M+2.y_M-12\right|}{\sqrt{3^2+2^2}}=\dfrac{\left|3.2+2.3-12\right|}{\sqrt{3^2+2^2}}=0\)

Để (d)//(d') thì \(\left\{{}\begin{matrix}3-m=2\\m-5\ne3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m\ne8\end{matrix}\right.\)
=>m=1
=>(d): y=(3-1)x+1-5=2x-4
Ta có: (d): y=2x-4; (d'): y=2x+3
Lấy A(3;2) thuộc (d)
=>KHoảng cách từ (d) đến (d') sẽ là khoảng cách từ A đến (d')
(d'): y=2x+3
=>2x-y+3=0
Khoảng cách từ A đến (d') là:
\(\dfrac{\left|2\cdot3+\left(-1\right)\cdot2+3\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{7}{\sqrt{5}}=\dfrac{7\sqrt{5}}{5}\)
=>\(d\left(\left(d\right);\left(d'\right)\right)=\dfrac{7\sqrt{5}}{5}\)

Đáp án C
Phương trình hoành độ giao điểm 2 x − 1 x+ 1 = 2 x − 3 ⇔ 2 x 2 − 3 x − 2 = 0 ⇔ x = 2 x = − 1 2
Vậy A ( 2 ; 1 ) ; B ( − 1 2 ; − 4 )
AB → = − 1 2 − 2 2 + − 4 − 1 2 = 5 5 2

a) Ta có: \(y=2x+1\)
\(+)a=2>0;b=1\)
Đồ thị hàm số cắt: \(Ox\left(-\dfrac{1}{2};0\right);Oy\left(0;1\right)\)
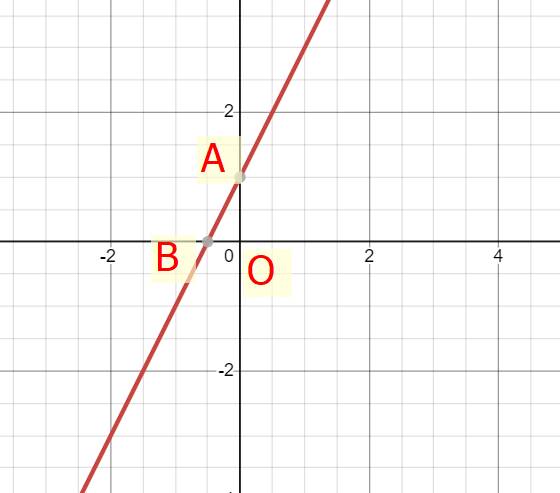
b) Gọi giao điểm của hàm số với trục Ox là B, với trục Oy là A
Xét tam giác OAB vuông tại O ta có: \(\left\{{}\begin{matrix}OA=1\\OB=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow S_{OAB}=\dfrac{1}{2}\cdot1\cdot\dfrac{1}{2}=\dfrac{1}{4}\left(đvdt\right)\)
c) Gọi khoảng cách từ O đến (d) là đường cao OH của tam giác OAB ta có:
\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)
\(\Rightarrow OH^2=\dfrac{OA^2OB^2}{OA^2+OB^2}=\dfrac{1^2\cdot\left(\dfrac{1}{2}\right)^2}{1^2+\left(\dfrac{1}{2}\right)^2}=\dfrac{1}{5}\)
\(\Rightarrow OH=\sqrt{\dfrac{1}{5}}=\dfrac{\sqrt{5}}{5}\)