Cho ABD có B D 61,1 , 42,8 0 0 . Hỏi góc A khoảng bao nhiêu độ? (số đo góc
làm tròn đến hàng đơn vị).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
0
Những câu hỏi liên quan
NH
0
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Ta có: \(\overrightarrow {BC} = \left( { - 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right)\)
\(\cos \widehat {ABC} = \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \frac{{\left( { - 7} \right).3 + 1.3}}{{\sqrt {{{\left( { - 7} \right)}^2} + {1^2}} .\sqrt {{3^2} + {3^2}} }} = - \frac{3}{5} \Rightarrow \widehat {ABC} \approx {126^o}\)
b) Ta có: \(\overrightarrow {BC} = \left( { - 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right),\overrightarrow {AC} = \left( { - 10; - 2} \right)\)
Suy ra: \(\begin{array}{l}AB = \left| {\overrightarrow {BA} } \right| = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \\AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{\left( { - 10} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt {104} \\BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{{\left( { - 7} \right)}^2} + {1^2}} = \sqrt {50} \end{array}\)
Vậy chu vi tam giác ABC là: \({P_{ABC}} = 2\sqrt {26} + 8\sqrt 2 \)
c) Để diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM thì M phải là trung điểm BC.
Vậy tọa độ điểm M là: \(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = \frac{{ - 9}}{2}\\\frac{{{y_B} + {y_C}}}{2} = \frac{3}{2}\end{array} \right.\). Vậy \(M\left( {\frac{{ - 9}}{2};\frac{3}{2}} \right)\)
3 tháng 8 2021
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
30 tháng 9 2021
B: Là vị trí thuyền hiện tại
D: là vị trí thuyền sau 10 phút
AC: chiều cao ngọn hải đăng = 63 m
Xét tg vuông ABC
\(\tan\widehat{ABC}=\tan19^o=\frac{AC}{AB}=\frac{63}{AB}\Rightarrow AB=\frac{63}{\tan19^o}\)
Xét tg vuông ACD có
\(\tan\widehat{ADC}=\tan54^o=\frac{AC}{AD}=\frac{63}{AD}\Rightarrow AD=\frac{63}{\tan54^o}\)
Quãng đường thuyền đi được sau 10' là
\(BD=AB-AD=\frac{63}{\tan19^o}-\frac{63}{\tan54^o}\)
24 tháng 1
a: Xét ΔABC và ΔDBC có
BA=BD
CB chung
CA=CD
Do đó: ΔABC=ΔDBC
=>\(\widehat{ABC}=\widehat{DBC}=60^0;\widehat{ACB}=\widehat{DCB}=50^0\)
\(\widehat{ABD}=\widehat{ABC}+\widehat{DBC}=60^0+60^0=120^0\)
\(\widehat{ACD}=\widehat{ACB}+\widehat{DCB}=50^0+50^0=100^0\)
b: Xét (B) có
\(\widehat{ABD}\) là góc ở tâm chắn cung AD
=>\(sđ\stackrel\frown{AD}=\widehat{ABD}=120^0\)
14 tháng 10 2014
tổng các góc trong tứ giác là:
A+B+C+D=360
mà A=3x;B=4x;C=x;D=2x)
suy ra 3x+4x+x+2x=360
x(3+4+1+2)=360
10x =360
x =360:10
x =36
CM
22 tháng 2 2018
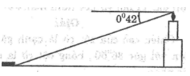
Chiều cao ngọn hải đăng là cạnh góc vuông đối diện với góc 0 ° 42 ' , khoảng cách từ tàu đến chân ngọn hải đăng là cạnh kề với góc nhọn.
Vậy khoảng cách từ tàu đến chân ngọn hải đăng là:
80.cotg 0 ° 42 ' ≈ 6547,76 (feet) ≈ 1,24 (hải lí)
24 tháng 12 2021
Gọi số người là x
Theo đề, ta có: \(x-7\in BC\left(12;18;30\right)\)
hay x=367