Cho x,y thỏa mãn x2+y2=1 tính gtln của x6+y6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

20 tháng 2 2018
Theo bđt Bunhiacopxki ta có : \(\left(x^2+y^2+z^2\right)\left(z^2+x^2+y^2\right)\ge\left(xy+yz+xz\right)^2\)
\(\Rightarrow x^2+y^2+z^2\ge\left|xy+yz+xz\right|\ge xy+yz+xz\)
\(\Leftrightarrow x^2+y^2+z^2+2xy+2yz+2xz\ge3\left(xy+yz+xz\right)\)
\(\Leftrightarrow\left(x+y+z\right)^2\ge3\left(xy+yz+xz\right)\)
\(\Rightarrow xy+yz+xz\le\dfrac{\left(x+y+z\right)^2}{3}=\dfrac{3^2}{3}=3\) có GTLN là 3
Dấu "=" xảy ra khi \(x=y=z=1\)
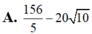
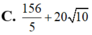


\(\le1\)