Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC. Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án cần chọn là: C
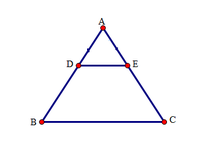
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.
Lại có A B C ^ = A C B ^ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

Đáp án cần chọn là: C
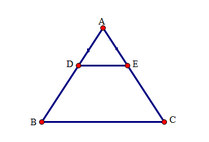
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.
Lại có A B C ^ = A C B ^ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

Đáp án cần chọn là: C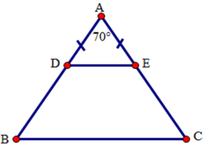
Tam giác ADE có AD = AE (gt) nen tam giác ADE cân tại A.
Suy ra A D E ^ = A E D ^ = 180 ° - D A E ^ ÷ 2 (1)
Tam giác ABC cân tại A (gt) nên A B C ^ = A C B ^ = 180 ° - B A C ^ ÷ 2 (2)
Từ (1) và (2) suy ra A D E ^ = A B C ^
Mà 2 góc và là hai góc ở vị trí đồng vị nên suy ra DE // BC
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang
Lại có A B C ^ = A C B ^ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

MDA = DAE = AEM = 90
=> ADME là hcn
Tam giác ABC vuông cân tại A
=> ACB = ABC = 45
mà MEC = 90
=> Tam giác EMC vuông cân tại E
=> EM = EC
mà DM = AE (ADME là hcn)
=> EM + DM = EC + AE = AC = 4 (cm)
PADME = 2 . (EM + DM) = 2 . 4 = 8 (cm)
DE = AM (ADME là hcn)
=> DE nhỏ nhất
<=> AM nhỏ nhất
<=> AM _I_ BC tại M
mà tam giác ABC vuông cân tại A
=> AM là đường trung tuyến
=> M là trung điểm
Vậy DE nhỏ nhất <=> M là trung điểm của BC.


Ta có \(DE=AM\ge AH\). Dấu " = " xảy ra khi \(M\equiv H\)
Vậy DE có độ dài nhỏ nhất là AH khi điểm M là trung điểm của BC.

Trong tam giác AD1E, có AD = AE(gt) nên tam giác AD1E là tam giác cân tại A
mà Â =50o => góc AD1E = \(\frac{180^0-Â}{2}=\frac{180^0-50^0}{2}=\frac{130^0}{2}=65^0\)(1)
Tam giác ABC cân tại A=> góc ABC \(=\frac{180^0-Â}{2}=\frac{180^0-50^0}{2}=\frac{130^0}{2}=65^0\)(2)
Từ (1), (2) => góc AD1E = ABC nên tứ giác BDEC là hình thang (ở vị trí đ/vị)
mà góc D1 +D2 =1800 ( kề bù), do đó D2 = 1800 - D1 = 1800 - 650 = 1150
Vậy góc D trong tứ giác BDEC = 1150
BDEC là hình thang cân