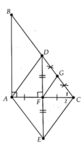
Cho tam giác ABC vuông tại A , kẻ trung tuyến AD ( D thuộc BC ) . Lấy điểm E đối xứng với A qua D . Tìm thêm điều kiện của tam giác ABC để tứ giác ABEC làhình vuông.A.Tam giác ABC cân tại A .B.Tam giá...

DT

Dấu tên

4 tháng 1 2022

Cho tam giác ABC vuông tại A , kẻ trung tuyến AD ( D thuộc BC ) . Lấy điểm E đối xứng với A qua D . Tìm thêm điều kiện của tam giác ABC để tứ giác ABEC làhình vuông.A.Tam giác ABC cân tại A .B.Tam giácABC có góc B bằng 60 độ .C.Tam giác ABC có góc B bằng 30 độ .D.Tam giác ABC có góc B bằng...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

4 tháng 1 2022

Chọn A

Đúng(0)

DT

Dấu tên

3 tháng 1 2022

Cho tam giác ABC vuông tại A , kẻ trung tuyến AD ( D thuộc BC ) . Lấy điểm E đối xứng với A qua D . Tìm thêm điều kiện của tam giác ABC để tứ giác ABEC làhình vuông.A.Tam giác cân tại .C.Tam giác có góc bằng .B.Tam giác có góc bằng .D.Tam giác có góc bằng...

Đọc tiếp

#Toán lớp 8

1

DT

Đỗ Tuệ Lâm

3 tháng 1 2022

tam giác phải có cạnh AB =AC

Đúng(0)

TN

Tâm Nhi Nguyễn Ngọc

3 tháng 1 2022

Cho tam giác ABC vuông tại A , kẻ trung tuyến ( )AD D BC . Lấy điểm E đối xứng với A qua D . Tìm thêm điều kiện của tam giác ABC để tứ giác ABEC làhình vuông.A.Tam giác ABC cân tại A . B.Tam giác ABC có góc B bằng 60.C.Tam giác ABC có góc B bằng 30 . D.Tam giác ABC có góc B bằng...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

3 tháng 1 2022

Chọn A

Đúng(1)

PT

Pham Trong Bach

12 tháng 9 2019

Cho tam giác ABC vuông tại A, kẻ trung tuyến AD (D ÎBC), gọi F là trung điểm của AC. Lấy điểm E đối xứng với A qua tâm D.a) Tứ giác ABEC là hình gì? Vì sao?b) Gọi G là trung điểm của DC. Tính độ dài FG, biết BC = 8cm.c) Tìm điều kiện của tam giác ABC để tứ giác ABEC là hình...

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

12 tháng 9 2019

a) Ta chứng minh ABEC là hình bình hành mà có Â = 90⁰ Þ tứ giác ABEC là hình chữ nhật.

b) Áp dụng định lý về đường trung bình của tam giác △ A D C ⇒ F G = 1 2 A D = 2 c m

c) Để tứ giác ABEC là hình vuông thì AB = AC ÞDABC phải là tam giác vuông cân tại A.

Đúng(0)

PT

Pham Trong Bach

30 tháng 12 2017

Cho tam giác ABC vuông tại A, kẻ trung tuyến AD (D Î BC), gọi F, G lần lượt là trung điểm của AC, DC. a) Tính độ dài FG, biết BC = 8 cm. b) Lấy điểm E đối xứng với D qua tâm F. Tìm điều kiện của tam giác ABC để tứ giác AECD là hình...

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

30 tháng 12 2017

a) Ta có AD = 1 2 B C = 8 2 = 4 c m

Xét DADC có GF là đường trung bình

⇒ G F = 1 2 A D = 4 2 = 2 c m

b) Chứng minh ADCE là hình thoi. Để ADCE là hình vuông thì điều kiện cần và đủ là E C D ^ = 90 0 ⇔ C 1 ^ = C 2 ^ = 45 0

Û DABC vuông tại A.

Đúng(0)

HN

Hương Nguyenthi

7 tháng 2 2021

Cho tam giác ABC cân tại A, trung tuyến AH. Lấy điểm D đối xứng với A qua H. CM tứ giác ABDC là hình thoi Qua A kẻ đường thẳng vuông góc với AH cắt tia DC tại E. Tứ giác ABCE là hình gì? Vì sao? Tìm điều kiện của tam giác ABC để tứ giác ABCE là hình thoi Gọi I là trung điểm của AE. CM AC, BE, HI đồng quy Kèm theo hình vẽ cho bài trên

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

7 tháng 2 2021

a) Xét tứ giác ABDC có

H là trung điểm của đường chéo BC(AH là đường trung tuyến ứng với cạnh BC trong ΔABC)

H là trung điểm của đường chéo AD(A và D đối xứng nhau qua H)

Do đó: ABDC là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Hình bình hành ABDC có AB=AC(ΔABC cân tại A)

nên ABDC là hình thoi(Dấu hiệu nhận biết hình thoi)

b) Ta có: ΔABC cân tại A(gt)

mà AH là đường trung tuyến ứng với cạnh đáy BC(gt)

nên AH là đường cao ứng với cạnh BC(Định lí tam giác cân)

\(\Leftrightarrow AH\perp BC\)

Ta có: AH\(\perp\)BC(cmt)

AH\(\perp\)AE(gt)

Do đó: BC//AE(Định lí 1 từ vuông góc tới song song)

hay HC//AE

Xét ΔAED có

H là trung điểm của AD(A và D đối xứng nhau qua H)

HC//AE(cmt)

Do đó: C là trung điểm của DE(Định lí 1 đường trung bình của tam giác)

Xét ΔAED có

H là trung điểm của AD(A và D đối xứng nhau qua H)

C là trung điểm của DE(cmt)

Do đó: HC là đường trung bình của ΔAED(Định nghĩa đường trung bình của tam giác)

\(\Leftrightarrow HC=\dfrac{AE}{2}\)(Định lí 2 về đường trung bình của tam giác)

mà \(HC=\dfrac{BC}{2}\)(H là trung điểm của BC)

nên AE=BC

Xét tứ giác ABCE có

AE//BC(cmt)

AE=BC(cmt)

Do đó: ABCE là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Đúng(3)

B

Bisconzo

18 tháng 10 2021

Cho tam giác ABC có đường trung tuyến AM, gọi N là trung điểm cạnh AC. Lấy điểm E đối xứng với M qua N. Tìm điều kiện của tam giác ABC để tứ giác AMCE là hình chữ nhật.Tam giác ABC vuông tại A Tam giác ABC cân tại A Tam giác ABC vuông tại B Tam giác ABC cân tại...

Đọc tiếp

#Toán lớp 8

0

LN

lê nguyễn hà chi

12 tháng 12 2021

Tam giác ABC vuông tại A có trung tuyến là AD, E là trung điểm AB, K
đối xứng của D qua E.
a) Chứng minh K đối xứng D qua AB
b) Tứ giác AKDC, ADBK là hình gì?
c) Cho BC = 8cm. Tính chu vi tứ giác ADBK
d) Tam giác ABC cần thêm điều kiện gì để ADBK là hình vuông v

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 12 2021

b: Xét tứ giác ADBK có

E là trung điểm của AB

E là trung điểm của DK

Do đó: ADBK là hình bình hành

mà DA=DB

nên ADBK là hình thoi

Đúng(0)

QC

Quynh Chi

21 tháng 9 2021

Bài 6: Cho tam giác ABC vuông tại A có trung tuyến là AD, E là trung điểm AB, K là điểm đối xứng của D qua E. a) Chứng minh K đối xứng với D qua AB b) Tứ giác AKDC, ADBK là hình gì? c) Tam giác ABC cần có thêm điều kiện gì để ADBK là hình vuông? d) Đường thẳng qua D vuông góc với AC cắt đường thẳng AK tại I. Tính diện tích của tứ giác BDIK theo diện tích của tam giác ABC.

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

21 tháng 9 2021

a: Ta có: ΔABC cân tại A

mà AD là đường trung tuyến ứng với cạnh huyền BC

nên \(AD=BD=CD=\dfrac{BC}{2}\)

Xét tứ giác ADBK có

E là trung điểm của đường chéo AB

E là trung điểm của đường chéo DK

Do đó: ADBK là hình bình hành

mà DA=DB

nên ADBK là hình thoi

Suy ra: K đối xứng với D qua AB

b: Xét ΔABC có

E là trung điểm của AB

D là trung điểm của BC

Do đó: DE là đường trung bình của ΔABC

Suy ra: DE//AC và \(DE=\dfrac{AC}{2}\)

mà \(DE=\dfrac{DK}{2}\)

nên DK//AC và DK=AC

hay AKDC là hình bình hành

Đúng(0)

VL

Vi Lê

12 tháng 11 2015 - olm

Cho tam giác ABC có trung tuyến AM. Gọi E là điểm đối xứng với A qua M.

a) Chứng minh tứ giác ABEC là HBH.

b) Khi tam giác ABC vuông tại A thì tứ giác ABEC là hình gì? Vì sao?

c) Tìm điều kiện của tam giác ABC để tứ giác ABEC là hình thoi.

#Toán lớp 8

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Cho tam giác ABC vuông tại A , kẻ trung tuyến AD ( D thuộc BC ) . Lấy điểm E đối xứng với A qua D . Tìm thêm điều kiện của tam giác ABC để tứ giác ABEC là
hình vuông.
A.Tam giác cân tại . C.Tam giác có góc bằng .	B.Tam giác có góc bằng . D.Tam giác có góc bằng .

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP