có bao nhiêu số tự nhiên có 3 chữ số, trong đó có đúng một chữ số 6 ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương án 1: Xét các số được lập có 3 chữ số lẻ, 3 chữ số chẵn trong đó không có số 0.
+ Bước 1: Chọn 3 số lẻ, có ![]() cách.
cách.
+ Bước 2: Chọn 3 số chẵn, có ![]() cách.
cách.
+ Bước 3: Xếp thứ tự 6 chữ số vừa lấy theo hàng ngang, có 6! = 720 cách.
Theo quy tắc nhân thì số các số trong phương án này là: 10.4.720 = 28800 số.
Phương án 2: Xét các số được lập có 3 chữ số lẻ, 3 chữ số chẵn trong đó có số 0.
Tương tự như trên, số các số tự nhiên trong phương án này là: ![]() số.
số.
Vậy số các số tự nhiên thỏa mãn yêu cầu là: 28800 + 36000 = 64800 số.
Chọn B.

Ai trả lời đúng thì mk sẽ tích cho nha
Nhanh lên mk đang cần gấp lắm !!

a) TH1 : Xét số thỏa yêu cầu kể cả chữ số đầu tiên bên trái =0
Chọn 3 chữ số lẻ có C35 cách
Chọn 3 chữ số chẵn có C35 cách
Sắp xếp 6 chữ số này có 6! cách
Vậy có C35 . C35 . 6! số
TH2 : Xét số có 6 chữ số thỏa mãn mà chữ số đầu tiên bên trái =0
Chọn 3 chữ số lẻ có C35 cách
Chọn 2 chữ số chẵn có C24 cách
Sắp xếp 5 chữ số có 5! cách
Vậy có C35 . C24 . 5! số
Vậy có C35 .C35. 6! - C35.C24.5! số tự nhiên gồm 6 chữ số khác nhau trong đó có 3 chữ số chẵn 3 chữ số lẻ

Ta có các số thỏa mãn đề bài là: 5ab,a5b,ab5(a,b khác 5)
Xét số có dạng 5ab có:
+1 cách chọn chữ số hàng trăm(5)
+9 cách chọn chữ số hàng chục(0,1,2,3,4,6,7,8,9)
+9 cách chọn chữ số hàng đơn vị(0,1,2,3,4,6,7,8,9)
=>Có các số dạng 5ab là:
1.9.9=81(số)
Xét số có dạng a5b có:
+8 cách chọn chữ số hàng trăm(1,2,3,4,6,7,8,9)
+1 cách chọn chữ số hàng chục(5)
+9 cách chọn chữ số hàng đơn vị(0,1,2,3,4,6,7,8,9)
=>Có các số dạng ab5 là:
8.1.9=72(số)
Xét số có dạng ab5 có:
+8 cách chọn chữ số hàng trăm(1,2,3,4,6,7,8,9)
+9 cách chọn chữ số hàng chục(0,1,2,3,4,6,7,8,9)
+1 cách chọn chữ số hàng đơn vị(5)
=>Có các số dạng ab5 là:
8.9.1=72(số)
Vậy có số số thỏa mãn đề bài là:
81+72+72=225(số)

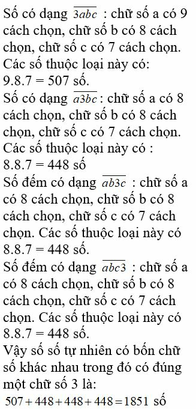
Số có dạng 3 a b c : chữ số a có 9 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có: 9.8.7 = 507 số.
Số có dạng a 3 b c : chữ số a có 8 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có : 8.8.7 = 448 số
Số đếm có dạng a b 3 c : chữ số a có 8 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có 8.8.7 = 448 số.
Số đếm có dạng a b c 3 : chữ số a có 8 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có 8.8.7 = 448 số.
Vậy số số tự nhiên có bốn chữ số khác nhau trong đó có đúng một chữ số 3 là: 507 + 448 + 448 +448 = 1851 số
Nhận xét: Bài toán yêu cầu có duy nhất (đúng một) số 3, các chữ số chỉ lặp lại có đúng 1 lần vì vậy khi giải toán cần đọc kỹ yêu cầu đề toán.