Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2. Biết SA = AB Mặt cầu ngoại tiếp hình chóp S.ABCD có thể tích bằng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Ta có R = S A 2 4 + R d 2 = a 2 + a 2 2 2 = a 3 2 ⇒ S = 4 π R 2 = 6 π a 2

Chọn D
Phương pháp: Xác định tâm của mặt cầu
ngoại tiếp khối chóp.



Đáp án D
Gọi O là tâm của hình chữ nhật ABCD và I là trung điểm của SC. Khi đó O I ⊥ ( A B C D )
⇒ I A = I B = I C = I D mà ∆ S A C vuông tại A I A = I S = I C . Do đó I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD suy ra I A = a 2 ⇒ S C = 2 a 2 . Mặt khác AC là hình chiếu của SC trên mặt phẳng A B C D ⇒ S C ; A B C D ^ = S C ; A C ^ = S C A ^ = 45 ° .Suy ra ∆ S A C vuông cân ⇒ S A = A C = 2 a ⇒ V S . A B C D = 1 3 . S A . S A B C D = 1 3 . 2 a . a . a 3 = 2 a 3 3 3 .

Chọn D.
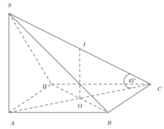
Phương pháp: Xác định tâm của mặt cầu ngoại tiếp khối chóp.
Cách giải: Gọi O là tâm của đáy. I là tâm của mặt cầu ngoại tiếp hình chóp. Dễ thấy I là trung điểm SC và S C A ^ = 45 °


Đáp án A
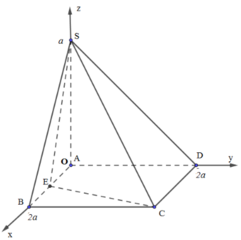
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2
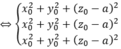
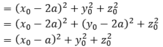
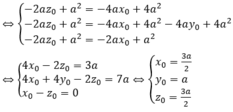
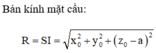
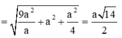
![]()

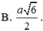
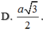

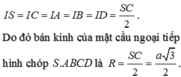
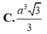
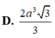
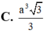
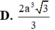

Gọi O là tâm đáy \(\Rightarrow OA=\dfrac{1}{2}AC=\sqrt{2}\)
\(\Rightarrow SO=\sqrt{SA^2-OA^2}=\sqrt{2}\)
\(\Rightarrow OA=OB=OC=OD=SO\Rightarrow\) O đồng thời là tâm mặt cầu ngoại tiếp chóp
\(\Rightarrow R=OA=\sqrt{2}\)
\(\Rightarrow V=\dfrac{4}{3}\pi R^3=\dfrac{8\pi\sqrt{2}}{3}\)