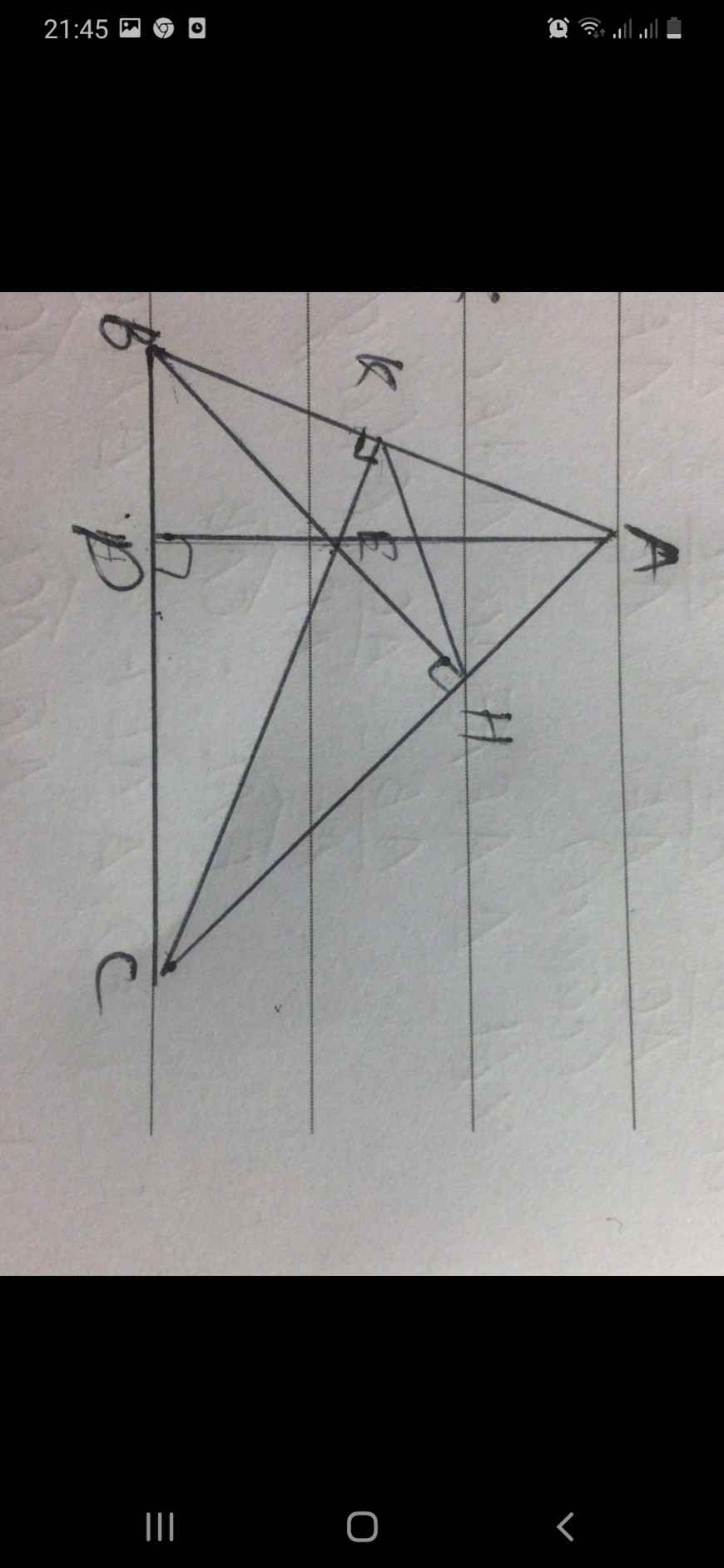
Cho \(\Delta\)ABC nhọn .Kẻ các đường cao BH và CK cắt nhau tại I .C/m BI.BH+CI.CK=BC2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 8 2021
a) Xét tứ giác AHIK có:
\(\widehat{AKI}+\widehat{AHI}=90^0+90^0=180^0\)
Nên tứ giác AHIK nội tiếp được trong một đường tròn(đpcm)
b) Vì CI vuông góc với AB(I là trực tâm tam giác ABC) và BD vuông góc với AB(góc nội tiếp chắn nửa đường tròn) nên CI // BD.
VÌ BI vuông góc với AC(I là trực tâm tam giác ABC) và CD vuông góc với AC(góc nội tiếp chắn nửa đường tròn) nên BI // CD.
Xét tứ giác BICD có:
CI // BD; BI // CD
Nên tứ giác BICD là hình bình hành.
Suy ra, BC và DI cắt nhau tại M là trung điểm của mỗi đoạn.
Xét tam giác AID có:
O là trung điểm của AD và M là trung điểm của DI nên OM là đường trung bình của tam giác AID.
Suy ra, AI // OM. Mà AI vuông góc với BC(do I là trực tâm tam giác ABC) nên OM vuông góc với BC(đpcm).
16 tháng 9 2021
\(\widehat{BKC}=\widehat{BHC}\left(=90^0\right)\) nên HKBC nội tiếp đường tròn
2 tháng 4 2022
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)
8 tháng 11 2015
Áp dụng hệ thức lượng trong 2 tam giác vuông MAC và NAB
ta có AM2 =AH.AC ; AN2 = AK.AB (1)
Mặt khác: 2 tam giác vuông HAB và KAC có góc A chung nên chúng đồng dạng
=> AB/AC = AH/AK => AH.AC = AK.AB (2)
Từ (1) và (2) => AM2 = AN2 hay AM = AN (dpcm)
8 tháng 11 2015
Bạn áp dụng hệ thức lượng nhé, hai góc gì đó đề bài cho bằng 90 độ sẽ tạo thành 2 tam giác vuông, còn 2 đường cao của tam giác nhọn lần lượt là 2 đường cao tương ứng của tam giác vuông đó. Sau đó áp dụng HTL thứ 1. Mình lười đánh máy quá nên chỉ ghi hướng làm thôi.