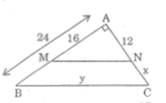
cho hình vẽ biết AB= 12CM, BC=16CM. TÍNH ĐỘ DÀI EF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong ΔABC, ta có: MN // BC (gt)
Suy ra: 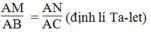
Suy ra: 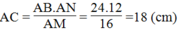
Vậy NC = AC – AN = 18 – 12 = 6(cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:
M N 2 = A M 2 + A N 2 = 16 2 + 12 2 = 400
MN = 20cm
Trong ΔABC, ta có: MN // BC (gt)
Suy ra:![]()
Vậy: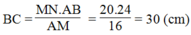

Xét hình thang ABCD có:
AE=DE (vì E là trung điểm của AD)
BF=FC (vì F là trung điểm của BC)
=> EF là đường trúng bình của hình thang ABCD
EF=(AB+DC):2
12=(AB+16):2
24=AB+16
8=AB
=> AB=8cm

a: Sửa đề; DH=16cm
DC=16+9=25cm
DB=căn DH^2+HB^2=20cm
BC=căn 12^2+9^2=15cm
b: Xét ΔDBC có
DC^2=DB^2+BC^2
nên ΔBDC vuông tại B
c: ΔBDC vuông tại B có sin C=BD/DC=4/5
nên \(\widehat{C}\simeq53^0\)
=>\(\widehat{B}\simeq180^0-53^0=127^0\)
Kẻ AK vuông góc DC
Xét tứ giác ABHK có
AB//HK
AK//HB
=>ABHK là hình bình hành
=>AK=BH=12cm
Xét ΔAKD vuông tại K có sin D=AK/AD=6/7
nên \(\widehat{D}\simeq59^0\)
=>góc A=180 độ-59 độ=121 độ
a: Sửa đề; DH=16cm
DC=16+9=25cm
DB=căn DH^2+HB^2=20cm
BC=căn 12^2+9^2=15cm
b: Xét ΔDBC có
DC^2=DB^2+BC^2 nên ΔBDC vuông tại B
c: ΔBDC vuông tại B có sin C=BD/DC=4/5 nên ˆ C ≃ 53*(*là độ C)
=> ˆ B ≃ 180* − 53* = 127*
Kẻ AK vuông góc DC
Xét tứ giác ABHK có: AB//HK AK//HB
=>ABHK là hình bình hành
=>AK=BH=12cm Xét ΔAKD vuông tại K có sin D=AK/AD=6/7 nên ˆ D ≃ 59*
=>góc A=180 độ-59 độ=121 độ

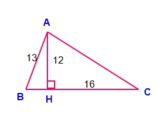
Áp dụng định lí Pi-ta-go trong ΔAHC vuông tại H ta có:
AC2 = AH2 + HC2 = 122 + 162 = 144 + 256 = 400
⇒ AC = 20 (cm)
Áp dụng định lí Pi-ta-go trong ΔAHB vuông tại H ta có:
BH2 + AH2 = AB2 ⇒ BH2 = AB2 - AH2 = 132 - 122 = 169 -144 = 25
⇒ BH = 5cm
Do đó BC = BH + HC = 5 + 16 = 21 (cm)

Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+16^2=400\)
hay AC=20(cm)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow HB^2=AB^2-AH^2=13^2-12^2=25\)
hay HB=5(cm)
Ta có: HB+HC=BC(H nằm giữa B và C)
nên BC=5+16=21(cm)
Vậy: AC=20cm; BC=21cm

AH \(\perp\) BC ( gt )
\(\Rightarrow\) Tam giác HAC vuông tại H
\(\Rightarrow\) \(^{AC^2}\) = \(^{AH^2}\) + \(^{HC^2}\)
\(\Rightarrow\) \(^{AC^2}\)= \(^{12^2}\) + \(^{16^2}\)
\(\Rightarrow\) \(^{AC^2}\)= 144 + 256
\(\Rightarrow\) \(^{AC^2}\)= 400
\(\Rightarrow\) AC = 20 ( cm )
AH \(\perp\) BC ( gt )
\(\Rightarrow\) Tam giác HAB vuông tại H
\(\Rightarrow\) \(AB^2\) = \(AH^2\) + \(BH^2\)
\(\Rightarrow\) \(BH^2\) = \(AB^2\) - \(AH^2\)
\(\Rightarrow\) \(BH^2\) = \(13^2\) - \(12^2\)
\(\Rightarrow\) \(BH^2\) = 169 - 144
\(\Rightarrow\) \(BH^2\) = 25
\(\Rightarrow\) BH = 5 ( cm )
Có: BH + HC = BC ( Vì H nằm giữa B và C )
\(\Rightarrow\) 5 + 16 = 21 ( cm )
Vậy AC = 20 cm
BC = 21 cm
Học tốt