Tính giá trị biểu thức sau:
C=x4+2x3y-2x3+x2y2-2x2y-x(x+y)+2x+3 tại x+y-2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 1 2022
\(x+y+1=0\\ \Leftrightarrow x+y=-1\)
Thay x+y=-1 vào C ta có:
\(C=x^2\left(x+y\right)-y^2\left(x+y\right)+x^2-y^2+2\left(x+y\right)+3\)
\(\Rightarrow C=x^2\left(-1\right)-y^2\left(-1\right)+x^2-y^2+2\left(-1\right)+3\)
\(\Rightarrow C=-x^2+y^2+x^2-y^2-2+3\)
\(\Rightarrow C=\left(-x^2+x^2\right)+\left(y^2-y^2\right)+\left(3-2\right)\)
\(\Rightarrow C=0+0+1\)
\(\Rightarrow C=1\)
CM
19 tháng 8 2018
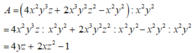
Giá trị biểu thức tại x = -2; y = 102; z= 102 là:
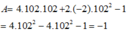
Chọn đáp án D
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 4 2023
A = 2\(x^2\)y + \(xy\) - 3\(xy\)
Thay \(x\) = -2; y = 4 vào biểu thức A ta có:
A = 2\(\times\) (-2)2 \(\times\) 4 + (-2) \(\times\) 4 - 3 \(\times\) (-2) \(\times\) 4
A = 2 \(\times\) 4 \(\times\) 4 - 8 + 6 \(\times\) 4
A = 8 \(\times\) 4 - 8 + 24
A = 32 - 8 + 24
A = 24 + 24
A = 48
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 4 2023
B = (2\(x^2\) + \(x\) - 1) - ( \(x^2+5x-1\) )
Thay \(x\) = - 2 vào biểu thức B ta có:
B = { 2\(\times\)(-2)2 + (-2) - 1} - { (-2)2 +5\(\times\)(-2) - 1}
B = { 2 \(\times\) 4 - 3} - { 4 - 10 - 1}
B = { 8 - 3} - { 4 - 11}
B = 5 - (-7)
B = 5 + 7
B = 12
CM
23 tháng 7 2019
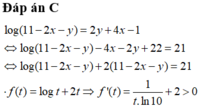
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
CM
17 tháng 4 2017
Đáp án C
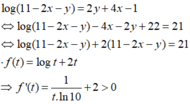
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
2 tháng 10 2021
Bài 2:
a: \(x^2\left(x^2-16\right)=0\)
\(\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
b: \(x^8+36x^4=0\)
\(\Leftrightarrow x^4=0\)
hay x=0
2 tháng 10 2021
a(b+3)-b(3+b)
=(3+b)(a-b)
Thay số, có: (3+1997).(2003-1997)
= 2000.6 =12000
xy(x+y)-2x-2y
xy(x+y)- 2(x+y)
(x+y).(xy-2)
Thay số, co: 7. (8-2)
7.4=28
PN
1
NA
2 tháng 3 2022
\(6x^2y^2+x^2y^2-4x^2y^2=\left(6+1-4\right)x^2y^2=3x^2y^2\)
Thay x=3, y=-1 vào biểu thức ta có:
\(3x^2y^2=3.3^2.\left(-1\right)^2=3.9.1=27\)
TC
15 tháng 4 2022
ta thay \(x=-\dfrac{1}{3};y=\dfrac{1}{2}\) vào biểu thức ta đc
\(2.\left(-\dfrac{1}{3}\right)^3-5.\left(-\dfrac{1}{3}\right)^2.\left(\dfrac{1}{2}\right)^2-2.\left(-\dfrac{1}{3}\right)^3\cdot\dfrac{1}{2}\)
\(=-\dfrac{2}{9}-5\cdot\dfrac{1}{9}\cdot\dfrac{1}{4}+\dfrac{2}{9}\cdot\dfrac{1}{2}\)
\(=-\dfrac{2}{9}-\dfrac{5}{36}+\dfrac{1}{9}=-\dfrac{1}{4}\)