cho 2 đoạn thẳng AB và BD cắt nhau tại trung điểm O ở mỗi đoạn . m và n theo thứ tự là trung điểm của AB và CD . CMR :O là trung điểm của MN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo https://h.vn/hoi-dap/question/147625.html nha

Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: 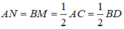
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: 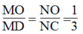
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: 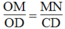 Hệ quả định lí Ta-lét)
Hệ quả định lí Ta-lét)
Suy ra: 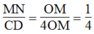
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
![]() (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Suy ra: ![]()
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)

mình ko biết cách c/m thẳng hàng ở câu c thôi ai giúp với

a) Xét \(\Delta AOC\) và \(\Delta BOD\) có :
AO = OB ( gt )
\(\widehat{O_1}=\widehat{O_2}\) ( đối đỉnh )
OC = OD ( gt )
=> \(\Delta AOC\) = \(\Delta BOD\) ( c.g.c)
=> AC = BD ( 2 cạnh tương ứng )
b)
=> \(\widehat{C_1}=\widehat{D_1}\) ( hai góc tương ứng )
=> AC // BD
c)
Kẻ MO cắt BD tại N'
Ta c/m được \(\Delta MOC=\Delta N'OD\left(g.c.g\right)\)(1)
=> N'D = MC
=> N'B = MA
=> N' trùng M
Mặt khác (1) => MO = ON
=> O là tung điểm của MN
Ta có hình vẽ
a/ Xét tam giác AOC và tam giác BOD có
-góc AOC = góc BOD (đối đỉnh)
-AO=OB (vì O là trung điểm của AB)
-CO=OD (Vì O là trung điểm của CD)
Vậy tam giác AOC = tam giác BOD
=> AC = BD (2 cạnh tương ứng)
b/ Xét tam giác AOD và tam giác BOC có
-góc AOD = góc BOC (đối đỉnh)
-AO=OB (vì O là trung điểm của AB)
-CO=OD (Vì O là trung điểm của CD)
Vậy tam giác AOD = tam giác BOC
=> góc DAB = góc ABC
Mà DAB; ABC : so le trong
=> AD//BC
c/ Vì tam giác AOC = tam giác BOD
=> góc OAC = góc OBD (2 góc tương ứng)
Xét tam giác AOM và BON có:
-góc OAC = góc OBD
-AM = BN (GT)
-AO=OB (O là trung điểm của AB)
Vậy tam giác AOM = tam giác BON
=> MO = ON (2 cạnh tương ứng)
Vậy O là trung điểm của MN (đpcm)