Cho góc xAy , phân giác az. Trên tia Ax lấy điểm B sao cho AB = 5cm. Qua B kẻ dường thẳng song song với Ay cắt Az tại C. Tính độ dài BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 11 2023
a:
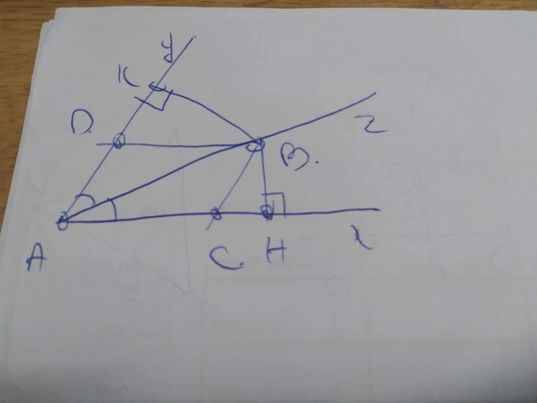
BD//AC
=>\(\widehat{DBA}=\widehat{BAC}\)(hai góc so le trong)(1)
CB//AD
=>\(\widehat{CBA}=\widehat{DAB}\)(hai góc so le trong)(2)
AB là phân giác của góc CAD
=>\(\widehat{CAB}=\widehat{DAB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{DBA}=\widehat{CBA}\)
Xét ΔACB và ΔADB có
\(\widehat{DBA}=\widehat{CBA}\)
BA chung
\(\widehat{CAB}=\widehat{DAB}\)
Do đó: ΔACB=ΔADB
=>AC=AD và BC=BD
b: Xét ΔAHB vuông tại H và ΔAKB vuông tại K có
AB chung
\(\widehat{HAB}=\widehat{KAB}\)
Do đó: ΔAHB=ΔAKB
=>BH=BK
c: Xét tứ giác AHBK có
\(\widehat{AHB}+\widehat{AKB}+\widehat{KAH}+\widehat{KBH}=360^0\)
=>\(\widehat{KBH}+60^0+90^0+90^0=360^0\)
=>\(\widehat{KBH}=360^0-90^0-90^0-60^0=120^0\)
24 tháng 11 2023
a:
b:
BD//AC
=>\(\widehat{DBA}=\widehat{BAC}\)(hai góc so le trong)(1)
CB//AD
=>\(\widehat{CBA}=\widehat{DAB}\)(hai góc so le trong)(2)
AB là phân giác của góc CAD
=>\(\widehat{CAB}=\widehat{DAB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{DBA}=\widehat{CBA}\)
Xét ΔACB và ΔADB có
\(\widehat{DBA}=\widehat{CBA}\)
BA chung
\(\widehat{CAB}=\widehat{DAB}\)
Do đó: ΔACB=ΔADB
=>AC=AD và BC=BD
c: Xét ΔAHB vuông tại H và ΔAKB vuông tại K có
AB chung
\(\widehat{HAB}=\widehat{KAB}\)
Do đó: ΔAHB=ΔAKB
=>BH=BK
d: Xét tứ giác AHBK có
\(\widehat{AHB}+\widehat{AKB}+\widehat{KAH}+\widehat{KBH}=360^0\)
=>\(\widehat{KBH}+60^0+90^0+90^0=360^0\)
=>\(\widehat{KBH}=360^0-90^0-90^0-60^0=120^0\)
TB
17 tháng 1 2016
sau khi đọc lời giải, nếu thấy đúng thì chúng ta kết bạn, okey?
THEO BÀI RA BC // AY
=> GÓC BCA=GÓC CAY
HAY GÓC BAC = GÓC ZAY (VÌ C THUỘC AZ) (1)
MÀ AZ LÀ P/G CỦA XAY
=> GÓC XAZ= GÓC ZAY (2)
NÊN TỪ (1) VÀ (2) => GÓC BCA= GÓC XAZ
HAY GÓC BAC= GÓC BCA (VÌ B THUỘC AX, C THUỘC AZ)
=> T/G ABC CÂN TẠI B
=> AB=BC
MÀ AB= 5 cm (GT)
=> BC= 5 cm
=> ĐPCM