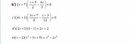
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(x^2-4x-5=\left(x-5\right)\left(x+1\right)\)
b: \(x^2-3x+2=\left(x-2\right)\left(x-1\right)\)
d: \(2x^2-3x+1=\left(x-1\right)\left(2x-1\right)\)
k: \(4x^2-9=\left(2x-3\right)\left(2x+3\right)\)


Câu 2:
Ta có: \(\sqrt{x^2-4x+4}=x-1\)
\(\Leftrightarrow2-x=x-1\left(x< 2\right)\)
\(\Leftrightarrow-2x=-3\)
hay \(x=\dfrac{3}{2}\left(tm\right)\)

b: Ta có: \(x\left(x+1\right)-\left(2x+3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-2x-3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\end{matrix}\right.\)
d: Ta có: \(\left(x-1\right)^2-4\left(x+2\right)^2=0\)
\(\Leftrightarrow\left(x-1-2x-4\right)\left(x-1+2x+4\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-1\end{matrix}\right.\)

Ta có: Khi khóa K đóng thì dòng điện sẽ không đi qua R2 nên số chỉ của Ampe kế là số chỉ của cường độ dòng điện chạy trong mạch, tức là khi khóa K đóng: 4A.
Hiệu điện thế giữa hai đầu đoạn mạch:
\(U=IR1=4.25=100V\)
Khi khóa K mở thì R1 nt R2, nên sẽ có cường độ dòng điện đi qua mạch, tức là cường độ dòng điện khi khóa K mở: 4A.
Điện trở tương đương: \(R=U:I=100:2,5=40\Omega\)
\(\Rightarrow R2=R-R1=40-25=15\Omega\)

Đặt \(\dfrac{x}{4}=\dfrac{y}{7}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k\\y=7k\end{matrix}\right.\)
Ta có: xy=112
\(\Leftrightarrow28k^2=112\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=4\cdot2=8\\y=7k=7\cdot2=14\end{matrix}\right.\)
Trường hợp 2: x=-2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=-8\\y=7k=-14\end{matrix}\right.\)

Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=30^0\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin30^0\)
\(\Leftrightarrow BC=4:\dfrac{1}{2}=8\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=8^2-4^2=48\)
hay \(AC=4\sqrt{3}\left(cm\right)\)

ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}




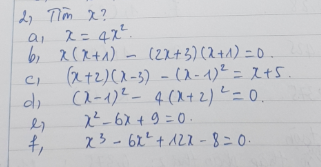
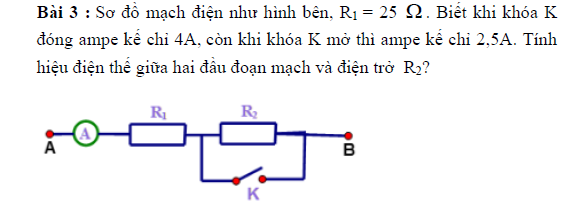


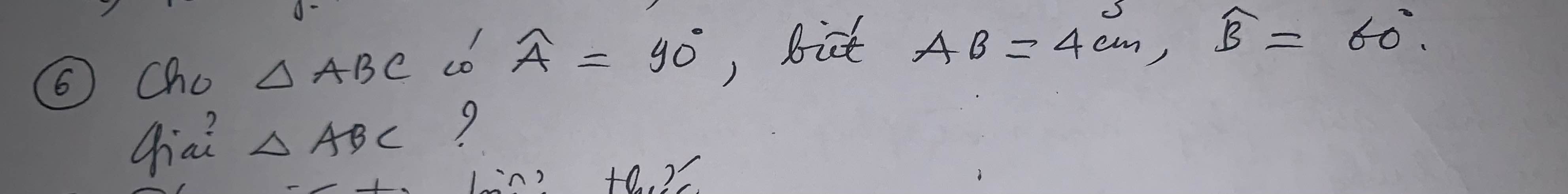




Trả lời:
b, \(\left(x+7\right)\left(\frac{x+5}{2}-\frac{4x}{3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+7=0\\\frac{x+5}{2}-\frac{4x}{3}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-7\\x=3\end{cases}}}\)
Vậy S = { -7; 3 }
Tự kết luận nghiệm nhé
b, \(\left(x+7\right)\left(\frac{x+5}{2}-\frac{4x}{3}\right)=0\)
TH1 : \(x+7=0\Leftrightarrow x=-7\)
TH2 : \(\frac{3x+15}{6}-\frac{8x}{6}=0\Leftrightarrow\frac{-5x+15}{6}=0\Leftrightarrow x=3\)
c, \(\left(4x+3\right)\left(\frac{3x+7}{4}-\frac{x-3}{12}\right)=0\)
\(\Leftrightarrow\left(4x+3\right)\left(\frac{9x-21}{12}-\frac{x-3}{12}\right)=0\)
TH1 : \(4x+3=0\Leftrightarrow x=-\frac{3}{4}\)
TH2 : \(\frac{9x-21-x+3}{12}=0\Leftrightarrow8x-18=0\Leftrightarrow x=\frac{9}{4}\)
d, \(\left(2x+1\right)\left(1-x\right)+2x=2\Leftrightarrow\left(2x+1\right)\left(1-x\right)+2\left(x-1\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(1-x\right)-2\left(1-x\right)=0\Leftrightarrow\left(1-x\right)\left(2x-1\right)=0\Leftrightarrow x=1;x=\frac{1}{2}\)
e, \(\left(x-2\right)\left(x^2-3x+5\right)=x^3-2x^2\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+5\right)-x^2\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(-3x+5\right)=0\Leftrightarrow x=2;x=-\frac{5}{3}\)