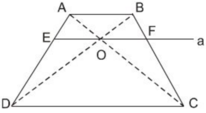
Cho hình thang ABCD có đáy AB =15m, đáy CD = 30m, chiều cao 30m. Một đường thẳng song song với 2 đáy, cắt AD và BC theo thứ tự tại E và F, chiều cao của hình thang CDEF bằng 10m.
a, Tính diện tích các tam giác ABF, CDF.
b, Tính diện tích 2 hình thang nhỏ