Cho 0\(\le\)a,b,c\(\le\)1.CMR: a+b+c-ab-bc-ca\(\le\)1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1N
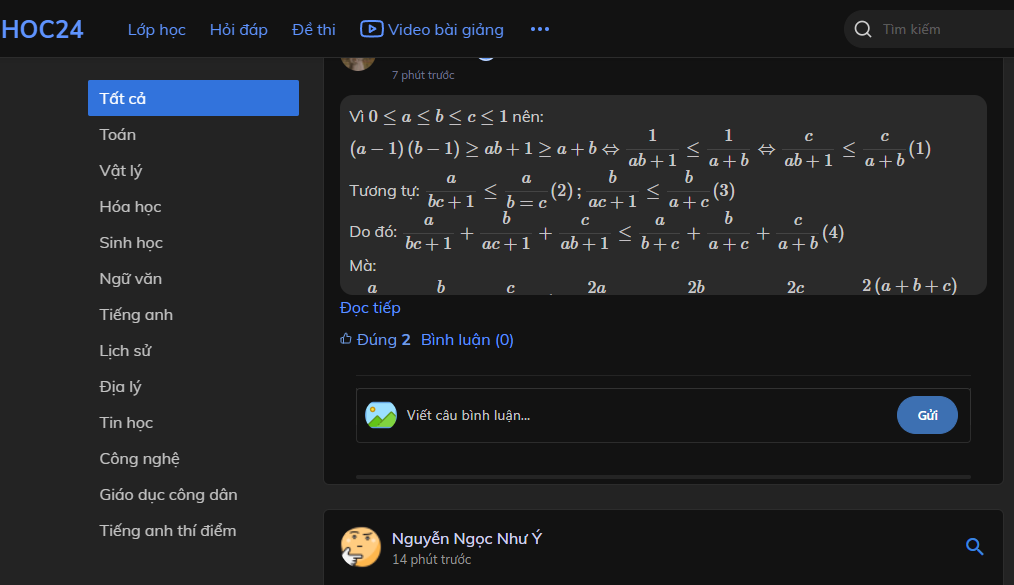
cho ba số dương \(0\le a\le b\le c\le1\) CMR \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le2\)
1
25 tháng 5 2022
Vì \(0\le a\le b\le c\le1\) nên:
\(\left(a-1\right)\left(b-1\right)\ge ab+1\ge a+b\Leftrightarrow\dfrac{1}{ab+1}\le\dfrac{1}{a+b}\Leftrightarrow\dfrac{c}{ab+1}\le\dfrac{c}{a+b}\left(1\right)\)
Tương tự: \(\dfrac{a}{bc+1}\le\dfrac{a}{b=c}\left(2\right);\dfrac{b}{ac+1}\le\dfrac{b}{a+c}\left(3\right)\)
Do đó: \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\left(4\right)\)
Mà: \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\le\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\left(5\right)\)
Từ (4) và (5) suy ra \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\left(đpcm\right)\)
LV
1
AH
Akai Haruma
Giáo viên
19 tháng 6 2021
Lời giải:
Vế đầu:
Áp dụng BĐT AM-GM:
$(ab+bc+ac)(a+b+c)\geq 9abc$
$\Leftrightarrow ab+bc+ac\geq 9abc$
$\Rightarrow ab+bc+ac-2abc\geq 9abc-2abc=7abc\geq 0$ do $a,b,c\geq 0$
Vế sau:
Áp dụng BĐT Schur:
$abc\geq (a+b-c)(b+c-a)(c+a-b)=(1-2a)(1-2b)(1-2c)$
$\Leftrightarrow 9abc\geq 4(ab+bc+ac)-1$
$\Rightarrow 2abc\geq \frac{8}{9}(ab+bc+ac)-\frac{2}{9}$
$\Rightarrow ab+bc+ac-2abc\leq ab+bc+ac-[\frac{8}{9}(ab+bc+ac)-\frac{2}{9}]=\frac{ab+bc+ac}{9}+\frac{2}{9}$
$\leq \frac{(a+b+c)^2}{27}+\frac{2}{9}$ (theo BĐT AM-GM)
$=\frac{1}{27}+\frac{2}{9}=\frac{7}{27}$
Ta có đpcm.
BH
1
28 tháng 5 2019
bạn tham khảo nhé : https://olm.vn/hoi-dap/detail/222370673956.html
1 tháng 3 2018
Áp dụng AM-GM:
\(ab+bc+ac\le\dfrac{\left(a+b+c\right)^2}{3}=\dfrac{0}{3}=0\)
BH
Cho a,b,c>0 và a+b+c=1. CMR: \(\frac{a-bc}{a+bc}+\frac{b-ca}{b+ca}+\frac{c-ab}{c+ab}\le\frac{3}{2}\)
1
28 tháng 5 2019
Ta có : a + bc = a ( a + b + c ) + bc = ( a + c ) ( a + b )
BĐT cần chứng minh tương đương với :
\(\frac{a\left(a+b+c\right)-bc}{\left(a+c\right)\left(a+b\right)}+\frac{b\left(a+b+c\right)-ca}{\left(b+c\right)\left(b+a\right)}+\frac{c\left(a+b+c\right)-ab}{\left(c+a\right)\left(c+b\right)}\le\frac{3}{2}\)
\(\left(a^2+ab+ac-bc\right)\left(b+c\right)+\left(ab+b^2+bc-ac\right)\left(a+c\right)+\left(ac+bc+c^2-ab\right)\left(a+b\right)\le\frac{3}{2}\left(a+b\right)\left(b+c\right)\left(a+c\right)\)
khai triển ra , ta được :
\(a^2b+ab^2+b^2c+bc^2+a^2c+ac^2+6abc\le\frac{3}{2}\left(a^2b+ab^2+b^2c+bc^2+a^2c+ac^2\right)+3abc\)
\(\Rightarrow\frac{-1}{2}\left(a^2b+ab^2+b^2c+bc^2+a^2c+ac^2\right)\le-3abc\)
\(\Rightarrow a^2b+ab^2+b^2c+bc^2+a^2c+ac^2\ge6abc\)( nhân với -2 thì đổi dấu )
\(\Rightarrow b\left(a^2-2ac+c^2\right)+a\left(b^2-2bc+c^2\right)+c\left(a^2-2ab+b^2\right)\ge0\)
\(\Rightarrow b\left(a-c\right)^2+a\left(b-c\right)^2+c\left(a-b\right)^2\ge0\)
vì BĐT cuối luôn đúng nên BĐT lúc đầu đúng
Dấu " = " xảy ra \(\Leftrightarrow\)\(a=b=c=\frac{1}{3}\)