K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
2 tháng 7 2021
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC
Trong (O) có BC là dây cung không đi qua O có D là trung điểm BC
\(\Rightarrow OD\bot BC\)
Tương tự \(\Rightarrow\left\{{}\begin{matrix}OE\bot AC\\OF\bot AB\end{matrix}\right.\)
Ta có: \(\angle ODB+\angle OFB=90+90=180\Rightarrow OFBD\) nội tiếp
Tương tự \(\Rightarrow OECD,OEAF\) nội tiếp
\(\Rightarrow\left(AFE\right),\left(BFD\right),\left(CDE\right)\) cùng đi qua điểm O là tâm đường tròn ngoại tiếp tam giác ABC
Xét \(\Delta ABC\) có E,F lần lượt là trung điểm AC,AB
\(\Rightarrow\) EF là đường trung bình \(\Rightarrow EF=\dfrac{1}{2}BC\)
Tương tự \(\Rightarrow\left\{{}\begin{matrix}DF=\dfrac{1}{2}AC\\DE=\dfrac{1}{2}AB\end{matrix}\right.\)
Xét \(\Delta AFE\) và \(\Delta FBD:\) Ta có: \(\left\{{}\begin{matrix}AF=BF\\AE=FD=\dfrac{1}{2}AC\\FE=BD=\dfrac{1}{2}BC\end{matrix}\right.\)
\(\Rightarrow\Delta AFE=\Delta FBD\left(c-c-c\right)\Rightarrow\left(AFE\right)=\left(FBD\right)\)
Tương tự \(\Rightarrow\left(CDE\right)=\left(AFE\right)\Rightarrow\left(AFE\right)=\left(FBD\right)=\left(CDE\right)\)
TN
18 tháng 7 2016
chắc đề thế này @@ (a+3)(9a-8) - (2+a)(9a-1)
=9a2-8a+27a-24-9a2-17a+2
=(9a2-9a2)+(-8a+27a-17a)-24+2
=2a-22.Thay a=-3,5 vào được:2*(-3,5)-22
=-7-22=-29.Đpcm
25 tháng 2 2017
A B C D E
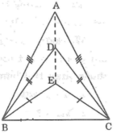
Vì AB = AC (gt) => A nằm trên đường trung trực của BC
Vì BD = DC (gt) => D nằm trên đường trung trực của BC
Vì BE = EC (gt) => E nằm trên đường trung trực của BC
=> A; D; E cùng nằm trên đường trung trực của BC
=> A ; D ; E thẳng hằng
CM
12 tháng 5 2017
Tam giác ABC cân tại A nên AB = AC
Khi đó A thuộc đường trung trực của BC (1)
Tam giác DBC cân tại D nên DB = DC
Khi đó D thuộc đường trung trực của BC (2)
Tam giác EBC cân tại E nên EB = EC
Khi đó E thuộc đường trung trực của BC (3)
Từ (1), (2) và (3) suy ra: A, D, E thẳng hàng.
13 tháng 3 2016
vì ước chung lớn nhất luôn là số nhỏ hơn hoặc bằng 1 trong 2 số đó
=> ước chung lớn nhất của tổng của chúng và bội chung nhỏ nhất của chúng
\(\frac{a}{ab+a+1}\)\(+\frac{b}{bc+b+1}+\frac{c}{ca+c+1}\)
\(=\frac{a}{ab+a+1}+\frac{ab}{a\left(bc+b+1\right)}+\)\(\frac{abc}{ab\left(ac+c+1\right)}\)
\(=\frac{a}{ab+a+1}+\frac{ab}{abc+ab+a}+\frac{abc}{abc.a+abc+ab}\)
\(=\frac{a}{ab+a+1}+\frac{ab}{1+ab+a}+\frac{1}{a+1+ab}\)(vì abc=1)
\(=\frac{ab+a+1}{ab+a+1}=1\)(điều phải chứng minh)
vậy nếu \(abc=1\)thì \(\frac{a}{ab+a+1}+\frac{b}{bc+b+1}+\frac{c}{ca+c+1}=1\)