Trong mặt phẳng Oxy cho điểm A (1,2) Viết phương trình đường thẳng đi qua ![]() cắt hai trục Ox,Oy lần lượt tại M và N( khác O) thỏa mãn ON = 2OM
cắt hai trục Ox,Oy lần lượt tại M và N( khác O) thỏa mãn ON = 2OM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp:
Viết phương trình đường thẳng dưới dạng phương trình đoạn chắn.
Cách giải:
![]()

Phương trình đường thẳng d có dạng:
\(y=kx-2k+1\)
Tọa độ A và B có dạng: \(A\left(\dfrac{2k-1}{k};0\right)\) ; \(B\left(0;-2k+1\right)\)
Để A, B nằm trên các tia Ox, Oy \(\Rightarrow\left\{{}\begin{matrix}\dfrac{2k-1}{k}>0\\-2k+1>0\end{matrix}\right.\) \(\Rightarrow k< 0\)
Khi đó ta có: \(S_{OAB}=\dfrac{1}{2}OA.OB=4\Leftrightarrow OA.OB=8\)
\(\Rightarrow\left(\dfrac{2k-1}{k}\right)\left(-2k+1\right)=8\)
\(\Leftrightarrow4k^2-4k+1=-8k\Leftrightarrow4k^2+4k+1=0\Rightarrow k=-\dfrac{1}{2}\)
Phương trình d: \(y=-\dfrac{1}{2}x+2\)

Chọn B
Gọi A (a; 0; 0), B(0; b; 0) và C(0; 0; c) với abc ≠ 0. Phương trình mặt phẳng (P) đi qua ba điểm A, B, C là
![]() .
.
Vì M(1;2;3) ∈ (P) nên ta có: ![]() .
.
Điểm M là trực tâm của tam giác ABC.
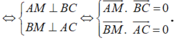

Phương trình mặt phẳng (P) là: ![]() <=> x + 3y + 2z - 14 = 0
<=> x + 3y + 2z - 14 = 0

Đáp án D
Ta có: OA → OB, OC => OA → (OBC) => OA → BC
Mặt khác vì AM → BC (M là trực tâm tam giác ABC) nên ta suy ra BC → (OAM) => BC → OM
Chứng minh tương tự ta được AC → OM. Do đó OM → (ABC). Ta chọn: n p → = OM → = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 2(y + 2) + 3(z - 3) = 0 ⇔ x - 2y + 3z - 14 = 0

Đường thẳng đó có phương trình trên đoạn chắn là
\(\dfrac{x}{a}+\dfrac{y}{b}=1\) (d)
Do d đi qua A(1; 2) ⇒ \(\dfrac{1}{a}+\dfrac{2}{b}=1\) (1)
M,N lần lượt là giao điểm của d vs Ox, Oy
⇒ \(\left\{{}\begin{matrix}OM=\left|a\right|\\ON=\left|b\right|\end{matrix}\right.\); Kết hợp giả thiết
⇒ |b| = 2|a|
⇒ \(\left[{}\begin{matrix}a=\dfrac{b}{2}\\a=\dfrac{-b}{2}\end{matrix}\right.\)
Nếu a = \(\dfrac{b}{2}\), kết hợp (1) ⇒ \(\left\{{}\begin{matrix}a=2\\b=4\end{matrix}\right.\)
Phương trình trên đoạn chắn là \(\dfrac{x}{2}+\dfrac{y}{4}=1\)
⇒ Phương trình tổng quát : 2x + y - 4 = 0
Nếu a = \(-\dfrac{b}{2}\) kết hợp (1) không có a,b
Vậy chỉ có 1 đường thẳng thỏa mãn đề bài
Đường thẳng đó có phương trình là
2x + y - 4 = 0