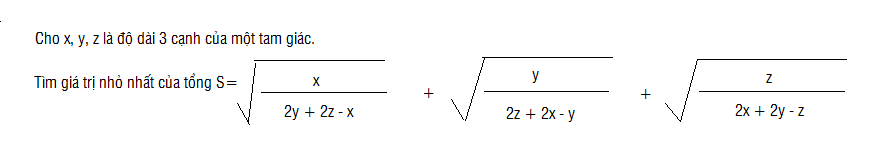
Mọi người giải hộ mình với ạ, đang cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NA
3
24 tháng 10 2021
\(\dfrac{2x-1}{3}=\dfrac{2-x}{-2}\)
\(\Rightarrow-2\left(2x-1\right)=3\left(2-x\right)\)
\(\Rightarrow-4x+2=6-3x\Rightarrow x=-4\)
DL
0
27 tháng 4 2022
Câu 3:
a)
CTPT xủa X là CnH2n+2O
\(n_{CO_2}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\Rightarrow n_{C_nH_{2n+2}O}=\dfrac{0,4}{n}\left(mol\right)\)
=> \(n_{H_2O}=\dfrac{\dfrac{0,4}{n}.\left(2n+2\right)}{2}=\dfrac{0,4}{n}\left(n+1\right)\left(mol\right)\)
Mà \(n_{H_2O}=\dfrac{9}{18}=0,5\left(mol\right)\)
=> n = 4
=> CTPT: C4H10O
b) \(n_{C_4H_{10}O}=\dfrac{0,4}{4}=0,1\left(mol\right)\)
=> m = 0,1.74 = 7,4 (g)
c)
(1) \(CH_3-CH_2-CH_2-CH_2OH\)
(2) \(CH_3-CH_2-CH\left(OH\right)-CH_3\)
(3) \(CH_3-C\left(CH_3\right)\left(OH\right)-CH_3\)
(4) \(CH_3-CH\left(CH_3\right)-CH_2OH\)
(5) \(CH_3-CH_2-CH_2-O-CH_3\)
(6) \(CH_3-CH\left(CH_3\right)-O-CH_3\)
(7) \(CH_3-CH_2-O-CH_2-CH_3\)
d)
X là \(CH_3-C\left(CH_3\right)\left(OH\right)-CH_3\) (2-metylpropan-2-ol)
NA
0
NH
1
2 tháng 12 2021
Bài 3.
Định luật ll Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\)
Gia tốc vật:
\(a=\dfrac{F-F_{ms}}{m}=\dfrac{4,5-\mu mg}{m}=\dfrac{4,5-0,2\cdot1,5\cdot10}{1,5}=1\)m/s2
Vận tốc vật sau 2s:
\(v=a\cdot t=1\cdot2=2\)m/s
PA
Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé
0
5 tháng 12 2021
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)
A
1
12 tháng 12 2021
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
Áp dụng BĐT cauchy, ta có:
\(\sqrt{\left(2y+2z-x\right)\cdot3x}\le\dfrac{2z+2y-x+3x}{2}=\dfrac{2\left(x+y+z\right)}{2}=x+y+z\\ \Leftrightarrow\sqrt{2y+2z-x}\le\dfrac{x+y+z}{\sqrt{3x}}\\ \Leftrightarrow\sqrt{\dfrac{x}{2y+2z-x}}\ge\dfrac{\sqrt{x}}{\dfrac{x+y+z}{\sqrt{3x}}}=\dfrac{x\sqrt{3}}{x+y+z}\)
\(\Leftrightarrow S=\sum\sqrt{\dfrac{x}{2y+2z-x}}\ge\sqrt{3}\left(\dfrac{x}{x+y+z}+\dfrac{y}{x+y+z}+\dfrac{z}{x+y+z}\right)\\ \Leftrightarrow S\ge\sqrt{3}\cdot\dfrac{x+y+z}{x+y+z}=\sqrt{3}\)
Dấu \("="\Leftrightarrow x=y=z\) hay tam giác đều