Rút gọn biểu thức: B = 1.2021+2.2020+3.2019+...+2021.1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT: \(\dfrac{1}{\sqrt{ab}}\ge\dfrac{2}{a+b}\) (dấu "=" xảy ra khi \(a=b\), nếu \(a\ne b\) thì \(\dfrac{1}{\sqrt{ab}}>\dfrac{2}{a+b}\)):
\(VT>\dfrac{2}{1+2021}+\dfrac{2}{2+2020}+\dfrac{2}{3+2019}+...+\dfrac{2}{2021+1}\)
\(VT>\dfrac{2}{2022}+\dfrac{2}{2022}+...+\dfrac{2}{2022}\) (2021 số hạng)
\(VT>\dfrac{1}{1011}.2021=\dfrac{2021}{1011}\) (đpcm)

a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.

\(a,ĐK:x\ne\pm1;x\ne0\\ M=\dfrac{1-x+2x}{\left(1+x\right)\left(1-x\right)}:\dfrac{1-x}{x}\\ M=\dfrac{x+1}{\left(x+1\right)\left(1-x\right)}\cdot\dfrac{x}{1-x}=\dfrac{x}{\left(1-x\right)^2}\\ b,ĐK:x\ge0;x\ne4\\ N=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ N=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Tất cả đều phải tìm điều kiện

a) a ≠ 0 , a ≠ − 5
b) Ta có A = a 3 + 4 a 2 − 5 a 2 a ( a + 5 ) = a ( a − 1 ) ( a + 5 ) 2 a ( a + 5 ) = a − 1 2
c) Thay a = -1 (TMĐK) vào a ta được A = -1
d) Ta có A = 0 Û a = 1 (TMĐK)

\(B=\dfrac{x}{x+2}-\dfrac{x^2+8}{x^2-4}+\dfrac{3}{x-2}\\ =\dfrac{x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{x^2+8}{\left(x-2\right)\left(x+2\right)}+\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{x^2-2x-x^2-8+3x+6}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{1}{x+2}\)

\(B=\dfrac{x}{x+2}-\dfrac{x^2+8}{x^2-4}+\dfrac{3}{x-2}\\ =\dfrac{x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{x^2+8}{\left(x-2\right)\left(x+2\right)}+\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{x^2-2x-x^2-8+3x+6}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{1}{x+2}\)
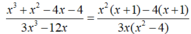
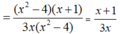
MỘT HHCN CÓ CHIỀU DÀI 25CM , CIỀU RỘNG BẰNG 3/5 CHIỀU DÀI. DIỆN TÍCH TÀN PHẦN LÀ 1750CM2 . TÍNH CHIỀU CAO