Cho đt tròn tâmo bán kính AB . Kẻ tiếp tuyến Ax, By với đt ( Ax và By thuộc cùng một nửa mặt phẳng bờ AB) a CM Ax song song với By
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét(O) có
CM,CA là tiếp tuyến
nên CM=CA và OC là phân giác của góc AOM(1)
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
CD=CM+MD
=>CD=AC+BD
c: AC*BD=CM*MD=OM^2=R^2 ko đổi
d: CM=CA
OM=OA
=>OC là trung trực của AM
mà H nằm trên trung trực của AM
nên O,H,C thẳng hàng

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC

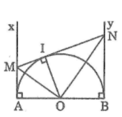
Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
O I 2 = MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = O I 2 = R 2

a: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM và OC là phân giác của góc AOM
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc BOM
=>\(\widehat{BOM}=2\cdot\widehat{MOD}\)
\(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOC}+2\cdot\widehat{MOD}=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
=>OC\(\perp\)OD
b: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
\(\dfrac{AC^2+BD^2}{CD^2}\)
\(=\dfrac{AC^2+\left(3AC\right)^2}{\left(CM+MD\right)^2}\)
\(=\dfrac{10AC^2}{\left(CA+BD\right)^2}\)
\(=\dfrac{10AC^2}{\left(AC+3AC\right)^2}=\dfrac{10}{4^2}=\dfrac{10}{16}=\dfrac{5}{8}\)

b: Xét (O) có
EK là tiếp tuyến
EA là tiếp tuyến
Do đó: EK=EA
Xét (O) có
FK là tiếp tuyến
FB là tiếp tuyến
Do đó: FK=FB
Ta có: EK+KF=EF
hay EF=AE+BF
Ta có: Ax⊥AB
By⊥AB
Do đó: Ax//By