Tìm tổng các nghiệm x của phương trình : x4 - 4x3 - x2 + 16x - 12 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)

Phương trình (1) vô nghiệm khi phương trình (2) có 2 nghiệm số âm hoặc vô nghiệm.
Nếu phương trình (2) có 2 nghiệm âm thì theo hệ thức Vi-ét ta có:
t 1 + t 2 = 13 > 0 vô lý
Vậy phương trình (1) vô nghiệm khi phương trình (2) vô nghiệm.
Suy ra: ∆ = 169 - 4m < 0 ⇔ m > 169/4}

Phương trình (1) có một nghiệm khi phương trình (2) có 1 nghiệm số kép bằng 0 hoặc phương trình (2) có một nghiệm bằng 0 và một nghiệm số âm.
Ta thấy, với ∆ = 0 phương trình (2) có nghiệm số kép t 1 = t 2 = 13/2 ≠ 0( không thỏa mãn)
Nếu phương trình (2) có một nghiệm t1 = 0. Theo hệ thức Vi-ét ta có:
t 1 + t 2 = 13 ⇔ t 2 = 13 - t 1 = 13 - 0 = 13 > 0 ( không thỏa mãn)
Vậy không có giá trị nào của m để phương trình (1) chỉ có 1 nghiệm.



Phương trình (1) có ba nghiệm phân biệt khi phương trình (2) có 1 nghiệm số dương và 1 nghiệm bằng 0 khi:
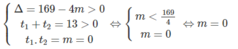


Phương trình (1) có hai nghiệm phân biệt khi phương trình (2) có nghiệm kép hoặc có 1 nghiệm dương và một nghiệm âm.
Phương trình (2) có một nghiệm số kép khi và chỉ khi Δ = 169 - 4m = 0
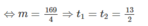
Phương trình (2) có một nghiệm số dương và một nghiệm số âm khi
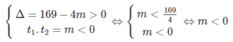
Vậy với m = 169/4 hoặc m < 0 thì phương trình (1) có 2 nghiệm phân biệt.


Phương trình (1) có 4 nghiệm phân biệt khi phương trình (2) có hai nghiệm số dương khi
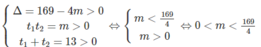

Đáp án là B.
Đặt t = x - 2 x Đạo hàm t , = 1 + 2 x 2 > 0
Do đó t ( 1 ) ≤ t ≤ t ( 2 ) , ∀ x ∈ [ 1 ; 2 ] , suy ra - 1 ≤ t ≤ 1
Ta có x 2 + 4 x 2 = t 2 + 4 , x 4 + 16 x 4 = ( x 2 + 4 x 2 ) 2 - 8 = ( t 2 + 4 ) 2 - 8 = t 4 + 8 t 2 + 8
Phương trình đã cho trở thành
t 4 + 8 t 2 + 8 - 4 ( t 2 + 4 ) - 12 t = m ⇔ t 4 + 4 t 2 - 12 t = m + 8 ( * )
Phương trình đã cho có nghiệm trong đoạn [1;2] khi và chỉ khi phương trình (*) có nghiệm trong [-1;1] Xét hàm số y=f(t)= t 4 + 4 t 2 - 12 t trên [-1;1]
Đạo hàm y , = 4 t 8 + 8 t - 12 , t ∈ ( - 1 ; 1 ) . y , = 4 ( t - 1 ) ( t 2 + t + 3 ) < 0 , ∀ t ∈ ( - 1 ; 1 )
Bảng biến thiên:
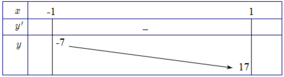
Do đó để phương trình đã cho có nghiệm trên [1;2] thì - 7 ≤ m + 8 ≤ 17 ⇔ - 15 ≤ m ≤ 9
Có 3 nghiệm 4;-1;1 Nên tổng là 4
Có tất cả 4 nghiệm