Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là trung điểm của AB, AC. Qua B kẻ đường thẳng song song với AC cắt tia NM tại D.a) Chứng minh tứ giác BDNC là hình bình hành.b) Tứ giác BDNH là hình gì? Vì sao?c) Gọi K là điểm đối xứng của H qua N. Qua N kẻ đường thẳng song song với HM cắt DK tại E. Chứng minh DE =...
Đọc tiếp
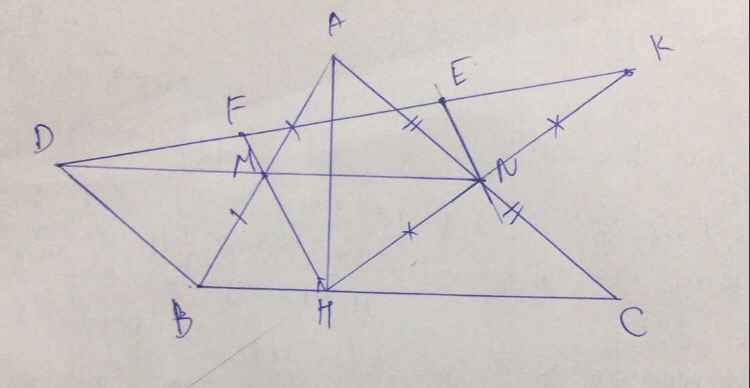
Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là trung điểm của AB, AC. Qua B kẻ đường thẳng song song với AC cắt tia NM tại D.
a) Chứng minh tứ giác BDNC là hình bình hành.
b) Tứ giác BDNH là hình gì? Vì sao?
c) Gọi K là điểm đối xứng của H qua N. Qua N kẻ đường thẳng song song với HM cắt DK tại E. Chứng minh DE = 2EK.
a) Xét \(\Delta ABC\)có: M là trung điểm AB, N là trung điểm AC => MN là đường trung bình \(\Delta ABC\)=> MN // BC
Xét tứ giác BDNC có: MN // BC; BD // NC => Tứ giác BDNC là hình bình hành
b) Xét tứ giác BDNH có: BH // ND => Tứ giác BDNH là hình thang
Vì BDNC là hình bình hành nên \(\widehat{BDN}=\widehat{BCN}\)(1)
Xét \(\Delta AHC\)vuông tại H có đường trung tuyến HN => HN = AN = CN => \(\widehat{HCN}=\widehat{CHN}\)(2)
Vì ND // BC nên \(\widehat{CHN}=\widehat{HND}\)(so le trong) (3)
Từ (1)(2)(3) => \(\widehat{BDN}=\widehat{HND}\)
Xét hình thang BDNH có \(\widehat{BDN}=\widehat{HND}\)=> BDNH là hình thang cân
c) Gọi I là giao điểm của DK và tia HM
Xét \(\Delta DEN\)có MI // NE; M là trung điểm ND => DI = IE
Xét \(\Delta KIH\)có NE // HI; N là trung điểm HK (H, K đối xứng với nhau qua N) => IE = EK
=> DI = IE = EK => DE = 2EK (ĐPCM)
Answer:
Vì M và N là trung điểm của AB và AC
=> MN là đường trung bình của tam giác BAC
=> MN // BC mà BD // CN
=> Tứ giác BDNC là hình bình hành
Vì \(\Delta AHC;AH\perp HC;NA=NC\Rightarrow HN=NA=NC\Rightarrow HN=BD\left(NC=BD\right)\)
=> Tứ giác BHND là hình thang cân có BH < BC = DN
Ta gọi HM ∩ DE = G
=> GM // EN
=> G là trung điểm của DE có M là trung điểm DN
=> DG = GE
Mà EN // GH, N là trung điểm của HK
=> E là trung điểm của GK
=> GE = EK
=> DG = GE = EK
=> DE = 2EK