Cho hai đường thẳng x'x và y'y cắt nhau tại điểm O. Trên x'x lấy ba điểm A, B, C sao cho OA=AB=BC, trên y'y lấy ba điểm E, M, N sao cho OE=OM=MN. Chứng minh rằng ba đường thẳng AE, BN và CM cùng đi qua một điểm.
Mn giúp mình với ạ, mình cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2021
Phương trình hoành độ giao điểm d1 và d2:
\(x-m+4=-x+3m-2\)
\(\Leftrightarrow2x=4m-6\)
\(\Rightarrow x=2m-3\Rightarrow y=m+1\)
Để giao điểm thuộc y=2x-3
\(\Rightarrow m+1=2\left(2m-3\right)-3\)
\(\Rightarrow m=\dfrac{10}{3}\)
15 tháng 11 2021
Ghi lại đề: \(y=\left(m+1\right)x-3;y=\left(2m-1\right)x+4\)
\(a,m=-\dfrac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{2}x-3\\y=-2x+4\end{matrix}\right.\)
Hệ số a 2 đt đã cho là \(\dfrac{1}{2};-2\) có tích là -1 nên 2 đt vuông góc
\(b,\Leftrightarrow\left(m+1\right)\left(2m-1\right)=-1\\ \Leftrightarrow2m^2+m-1=-1\\ \Leftrightarrow2m^2+m=0\\ \Leftrightarrow m\left(2m-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{1}{2}\end{matrix}\right.\)
HQ
Hà Quang Minh
Giáo viên
13 tháng 1
a)
* Xét đường thẳng y = x
Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x
Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1)\
* Xét đường thẳng y = -x + 2
Cho x = 2 thì y = -2 + 2 = 0 nên điểm (2; 0) thuộc đường thẳng y = - x+ 2
Cho y = 2 suy ra x = 0 nên điểm (0; 2 ) thuộc đường thẳng y = -x + 2
Đường thẳng y = - x + 2 đi qua hai điểm (2; 0) và (0; 2)
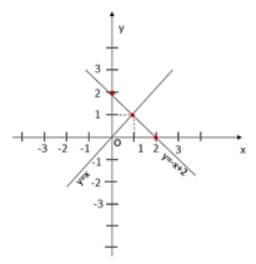
b) Giao điểm A của hai đường thẳng đã cho là A(1;1)
c) Cho y =0 ta được −x + 2 = 0 hay x = 2, suy ra B(2; 0).
Gọi C là giao điểm của đường thẳng y = −x + 2 và trục Oy. Suy ra C(0; 2). Dễ thấy tam giác OBC vuông cân tại O (vì OB = OC = 2).
Xét hai tam giác OAB và OAC có:
cạnh OA chung;
OB = OC;
\( \widehat {OBA} = \widehat {OCA} = 45^0\)
Do đó \(\Delta OAB = \Delta OAC\), từ đó suy ra AB = AC.
Điều này chứng tỏ A là trung điểm của BC, mà \(\Delta OBC \) cân tại O nên \(OA \bot AB\), tức là \(\Delta OAB\) vuông tại A.
d)
Đường thẳng y = x có hệ số góc bằng 1.
Đường thẳng y = - x + 1 có hệ số góc bằng -1
Tích của hai hệ số góc bằng -1
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 4 2020
Để 2 đường thẳng trùng nhau \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m=m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m=\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng song song \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m\ne m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m\ne\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng cắt nhau \(\Rightarrow2k+6\ne-3\Rightarrow k\ne-\frac{9}{2}\)
Để 2 đường thẳng vuông góc \(\Rightarrow\left(2k+6\right).\left(-3\right)=1\Rightarrow k=-\frac{19}{6}\)
CM
21 tháng 2 2017
Hai đường thẳng lần lượt có các vectơ chỉ phương là u 1 = 1 ; 3 và u 2 = − 1 ; 2 nên ta có cos d 1 , d 2 = cos u 1 → , u 2 → = 1. − 1 + 3.2 1 2 + 3 2 . − 1 2 + 2 2 = 1 2 .
Do đó góc giữa hai đường thẳng là α = 45 ° . Đáp án là phương án B.