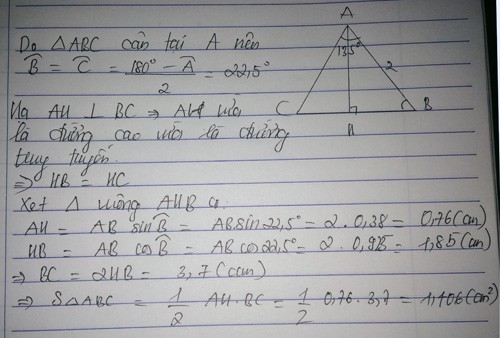Tam giác ABC có ABC=135 độ. BC=2cm. AB=\(\sqrt{2}\). Tìm AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
JA
0
T
10 tháng 3 2019
( bạn tự vẽ hình)
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
I
22 tháng 2 2020
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
15 tháng 2 2018
Tự vẽ hình nhé trả lời hóng giao thừa thôi :))
vì BE vuông góc BD nên BE là đường phân giác ngoài của tam giác ABC.
theo tính chất đường phân giác (ngoài) ta có :
\(\frac{AE}{AB}=\frac{EC}{BC}\)\(\Rightarrow\)\(CE=\frac{AC.BC}{AB}\)
\(\Rightarrow\)\(CE=\frac{AE.2}{3}\)
\(\Rightarrow\)\(3CE=\left(CE+AC\right).2\)
\(\Rightarrow\)\(3CE=2CE+2AC\)
\(\Rightarrow\)\(CE=2.AC=6\left(cm\right)\)