Bài 3. (1 điểm). Xác định a để đa thức f(x)=x^3 –4x^2 +6x− a chia hết cho đa thức g(x)=x-2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1:
1.
$A=(x-2)^2+6x+5=x^2-4x+4+6x+5=x^2+2x+9$
2.
$B=\frac{15x^2y^3}{5x^2y^2}-\frac{10x^3y^2}{5x^2y^2}+\frac{5x^2y^2}{5x^2y^2}$
$=3y-2x+1$
Bài 3:
$f(x)=x+4x^2-5x+3=4x^2-4x+3=4x(x-3)+8(x-3)+27$
$=(x-3)(4x+8)+27=g(x)(4x+8)+27$
Vậy $f(x):g(x)$ có thương là $4x+8$ và dư là $27$


Bài 3:
\(\dfrac{f\left(x\right)}{g\left(x\right)}=\dfrac{x^4+ax^2+b}{x^2-3x+2}\)
\(=\dfrac{x^4-3x^3+2x^2+3x^3-9x^2+6x+\left(a+7\right)x^2-3x\left(a+7\right)+2\left(a+7\right)+x\left(-6+3a+7\right)+b-2a-14}{x^2-3x+2}\)
Để đây là phép chia hết thì 3a+1=0 và b-2a-14=0
=>a=-1/3; b=2a+14=-2/3+14=40/3

x^4+6x^3+7x^2-6x+a=x^4+2.3x.x^2+9x^2-6x-2x^2+a
=(x^2+3x)^2-2(3x+x^2)+a=(3x+x^2)(x^2+3x-2)+a
vậy a=3(3x+x^2)
tôi chịu, sai thì... T.T

-Áp dụng định lí Bezout:
\(P\left(-1\right)=\left(-1\right)^4-6.\left(-1\right)^3+7.\left(-1\right)^2+a.\left(-1\right)+b=0\)
\(\Rightarrow1+6+7-a+b=0\)
\(\Rightarrow a-b=14\left(1\right)\)
\(P\left(-2\right)=\left(-2\right)^4-6.\left(-2\right)^3+7.\left(-2\right)^2+a.\left(-2\right)+b=0\)
\(\Rightarrow16+48+28-2a+b=12\)
\(\Rightarrow2a-b=80\left(2\right)\)
-Từ (1) và (2) suy ra: \(a=66;b=52\)
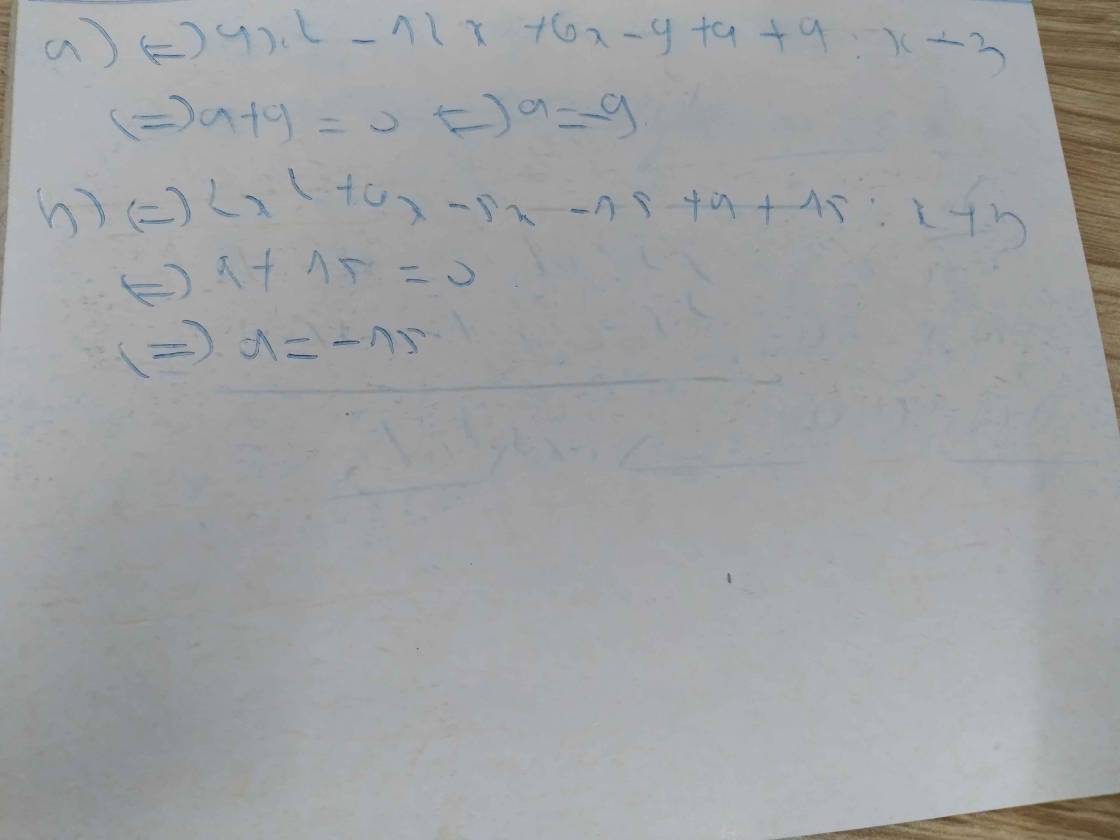
\(\Leftrightarrow x^3-2x^2-2x^2+4x+2x-4-a+4⋮x-2\)
hay a=4