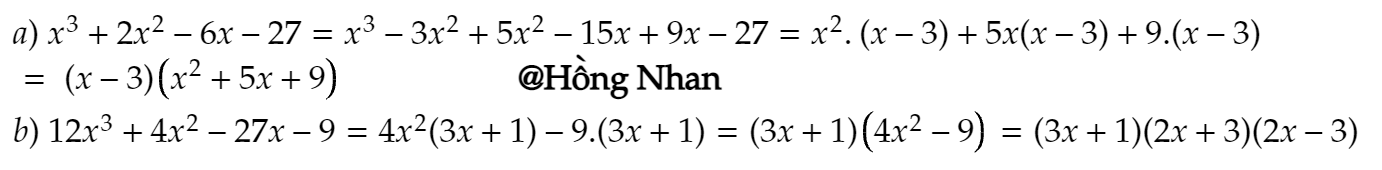CTR: đa thức f(x)=25x2+20x+11 không có nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
3
27 tháng 3 2017
\(f\left(x\right)=x^2+2x+3\)
\(\Leftrightarrow x^2+2x+1+2\)
\(\Leftrightarrow\left(x+1\right)^2+2\)
Vì \(\left(x+1\right)^2\ge0\)=>\(\left(x+1\right)^2+2\ge2\)
Vậy PT ko có nghiệm
27 tháng 3 2017
\(x^2+2x+3=0\)
\(\Rightarrow x^2+2x+1+2=0\)
\(\Rightarrow\left(x+1\right)^2+2=0\)( vô lý )
=> Đa thức vô nghiệm
NT
3
22 tháng 5 2017
f(x)=x2−x−x+2
x là nghiệm của đa thức f(x)
x2−x−x+1+1=0
x.(x-1)-(x-1)+1=0
(x-1).(x-1)+1=0
(x-1)2+1=0
=>(x-1)2=-1 (vô lý)
Vậy đa thức f(x) không có nghiệm
22 tháng 5 2017
Ta có : f(x) = x2 - x - x + 2 = x2 - x - x + 1 + 1
= x(x - 1) - (x- 1) +1
= (x - 1) 2 + 1 \(\ge\)1 > 0
Vậy f(x) vô nghiệm .
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
2 tháng 8 2023
\(a,36-4x^2+20xy-25y^2\\ =36-\left(4x^2-20xy+25y^2\right)\\ =6^2-\left[\left(2x\right)^2-2.2x.5y+\left(5y\right)^2\right]\\ =6^2-\left(2x-5y\right)^2\\ =\left[6-\left(2x-5y\right)\right]\left[6+\left(2x-5y\right)\right]\\ =\left(6-2x+5y\right).\left(6+2x-5y\right)\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
2 tháng 8 2023
a/
\(=6^2-\left[\left(2x\right)^2-2.2x.5y+\left(5y\right)^2\right]=\)
\(6^2-\left(2x-5y\right)^2=\left[6-\left(2x-5y\right)\right].\left[6+\left(2x-5y\right)\right]\)
24 tháng 4 2016
Ta có : x2 + 6x + 10 = x2 + 6x + 9 + 1 = ( x2 + 6 + 9 ) + 1
= ( x + 3 )2 + 1
Vì (x+3)2\(\ge\) 0 =) (x+3)2+1\(\ge\) 1
=) (x+3)2+1>0
Vậy x2 - 6x + 10 ko có nghiệm
13 tháng 5 2020
Bài làm
a) \(P=\left(-\frac{2}{3}x^3y^2\right)\left(\frac{1}{2}x^2y^5\right)\)
\(P=\left(-\frac{2}{3}.\frac{1}{2}\right)\left(x^3y^2x^2y^5\right)\)
\(P=-\frac{1}{3}x^5y^7\)
- Hệ số của P là -1/3
- Biến của P là x5y7
b) *) Thay x = 3 vào đa thức M(x) ta đuợc:
M(3) = 32 - 4.3 + 3
=> M(3) = 9 - 12 + 3
=> M(3) = 0
Vậy đa thức M(x) có nghiệm là x = 3.
*) Thay x = -1 vào đa thức M(x), ta được:
M(3) = (-1)2 - 4.(-1) + 3
=> M(3) = 1 + 4 + 3
=> M(3) = 8
Vậy x = -1 không là nghiệm của đa thức M(x) ( đpcm )
# Học tốt #